

Inhaltsverzeichnis:
2.2. Prinzipieller Aufbau und Funktionsweise eines SBS-Oszillators
2.3. Resonatorberechnung eines Lasers mit phasenkonjugierendem SBS-Spiegel
3.1.2 Variation der Startresonatorlänge
3.1.3 Variation der Verluste im Startresonator
3.1.4 Variation der Fokussierung in der SBS-Zelle
4.1.2. Transientes Modenverhalten
4.1.3. Auswirkungen auf die Zeitstruktur der Pulse
4.2.2. Transientes Modenverhalten mit SF6 als SBS-Medium
4.2.3. Auswirkungen auf die Zeitstruktur der Pulse
4.3.2. Auswirkungen auf die Zeitstruktur der Pulse
4.4.2. Auswirkungen auf die Zeitstruktur der Pulse
4.5.1. Energiereflexion in Abhängigkeit von den Verlusten im Startresonator
4.5.2. Verluste am Pinhole mit und ohne Aberrator im SBS-Resonator
4.5.3. Leistungsreflexion der SBS
4.5.4. Abschätzung zur Schwellabsenkung der SBS im Resonator
5. Zusammenfassung und Diskussion der Ergebnisse
Immer mehr Laseranwendungen, insbesondere in der Materialbearbeitung, verlangen hohe mittlere Ausgangsleistungen bei sehr guter Stahlqualität und niedrigen Kosten.
Die Strahlqualität von Festkörperlasern hoher mittlerer Ausgangsleistungen wird entscheidend durch thermisch induzierte Doppelbrechung und Aberrationen der thermische Linse des stark gepumpten aktiven Mediums bestimmt. Zur Kompensation der Aberrationen der thermischen Linse und des Astigmatismus doppelbrechender Lasermedien, können phasenkonjugierende Spiegel eingesetzt werden. Verfahren für die Erzeugung phasenkonjugierender Spiegel [1] sind zum Beispiel die Vier-Wellen-Mischung (FWM) [2, 3, 4], die Brillouin gestützte Vier-Wellen-Mischung (BEFWM) [5] und die stimulierte Brillouin-Streuung (SBS) [6, 7].
Phasenkonjugierende Spiegel auf der Basis der stimulierten Brillouin-Streuung finden schon vielfach in Oszillator-Verstärker-Systemen mit mittleren Ausgangsleistungen bis zu 870 Watt Anwendung [8, 9, 10, 11, 12]. Die SBS eignet sich auch für den Einsatz als passiver Güteschalter und phasenkonjugierender Spiegel zur Erzielung sehr guter Strahlqualitäten in Laser-Oszillatoren. Mit SBS-Oszillatoren wurden bisher mittlere Ausgangsleistungen von bis zu 27 Watt erreicht [13]. Dabei nutzt man die Möglichkeit der Schwellherabsetzung der SBS in längenabgestimmten Oszillatoren aus [14].
Die Kopplung von Startresonator und SBS-Resonator spielt für
die Ausbildung der longitudinalen Modenstruktur eine bedeutende
Rolle [15, 16]. Der Einfluß der Resonatorparameter
auf die Modenstruktur und die Ausgangsparameter sind in dieser
Arbeit untersucht worden. Dafür sind die Abhängigkeiten
der Pulsenergie, der Pulsstabilität und der longitudinalen
Modenstruktur des Laserlichts von der Längenanpassung des
SBS-Resonators und des Startresonators an die durch die SBS hervorgerufene
Frequenzverschiebung des Lichts (Brillouin-Shift) sowie von der
Reflektivität des hinteren Startresonatorspiegels und von
der Fokussierung in den SBS-Medien SF6, CO2
und Xenon untersucht worden. Weiterhin wurde in ersten Experimenten
die Qualität der Phasenkonjugation im SBS-Resonator und die
Reflektivität des SBS-Spiegels in Abhängigkeit des effektiven
Reflexionsgrades des Startresonatorspiegels für verschiedene
Aberrationen untersucht. Aus den Meßergebnissen können
Rückschlüsse auf den Schaltprozeß der SBS gezogen
werden. Weiterhin kann das Resonatordesign optimiert werden.
2.1. Phasenkonjugierende SBS-Spiegel
Ursache für die stimulierte Brillouin-Streuung (SBS) ist
die nichtlineare Wechselwirkung des einfallenden Lichts hoher
Intensität mit dem SBS-Medium. Die Polarisation 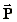 des Mediums hängt dann nicht mehr linear von der elektrischen
Feldstärke
des Mediums hängt dann nicht mehr linear von der elektrischen
Feldstärke 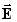 des einfallenden Lichtes
ab, die Komponenten Pi des Polarisationsvektors enthalten
additive Terme
des einfallenden Lichtes
ab, die Komponenten Pi des Polarisationsvektors enthalten
additive Terme 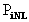 .
.
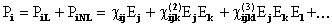 (1)
(1)
Die SBS ist ein nichtlinearer Effekt 3. Ordnung, was bedeutet,
daß die 3. Potenz der elektrischen Feldstärke den entscheidenden
Anteil der Polarisation liefert. 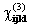 ist
der Suszeptibilitätstensor 3. Ordnung. Die aus den Maxwell-Gleichungen
resultierende Wellengleichung der nichtlinearen Optik [17],
ist
der Suszeptibilitätstensor 3. Ordnung. Die aus den Maxwell-Gleichungen
resultierende Wellengleichung der nichtlinearen Optik [17],
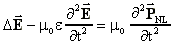 (2)
(2)dient der Beschreibung des elektrischen Feldes in nichtlinearen, homogenen und isotropen Medien. Der Mechanismus der Wechselwirkung zwischen einfallendem und reflektiertem Licht ist eine Dichtemodulation im SBS-Medium, die durch die Schwebung aus einfallendem und gestreutem Licht via Elektrostriktion gebildet wird. Die Kraftwirkung auf die Moleküle des SBS-Mediums ist dabei proportional zum Quadrat der elektrischen Feldstärke [18].
Die stimulierte Brillouin-Streuung kann auch als Photon-Phonon-Wechselwirkung
betrachtet werden. Dabei wird durch einen unelastischen Stoß
ein akustisches Phonon erzeugt unter Richtungsumkehr des auslösenden
Photons (Stokes-Streuung). Aufgrund der Energieerhaltung besitzt
das reflektierte Licht eine geringere Energie als das einfallende,
damit auch eine kleinere Frequenz. Diese Frequenzdifferenz wird
auch als Brillouin-Shift nB
bezeichnet, sie hat entscheidende Bedeutung für den stimulierten
Streuprozeß. Eine andere Möglichkeit der Brillouin-Streuung
ist die Vernichtung eines akustischen Phonons unter Richtungsumkehr
des einfallenden Lichtes. Das reflektierte Licht besitzt dann
eine um nB erhöhte
Frequenz (Anti-Stokes-Streuung). Abb. 2.1.1 zeigt beide Streuprozesse
in einer Gegenüberstellung.
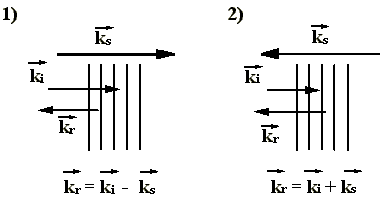
Abb. 2.1.1: Prinzipskizze der Brillouin-Streuung: 1) Stokes-Streuung
2) Anti-Stokes-Streuung
Für die gestreute Welle ergibt sich nach dem Impulserhaltungs-
und Energieerhaltungssatz für die Frequenz n
und den Wellenvektor 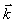 :
:
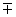 nB
nB
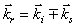 (3)
(3)Der Index r steht für reflektiert, i für einfallend und s für Schallwelle. Da die Impulse der einfallenden und reflektierten Lichtwelle nur wenig voneinander abweichen [18], kann folgende Näherung gemacht werden:
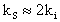 (4)
(4)Der Prozeß der stimulierten Brillouin-Streuung kann im Wellenbild wie folgt beschrieben werden.
Das in ein SBS-Medium einfallende Licht wird zunächst an statistisch verteilten Schall-wellen in alle Richtungen gestreut. Diese Dichtefluktuationen entstehen aufgrund der Brownschen Molekularbewegung und sind temperaturabhängig. Die in entgegengesetzter Richtung zur einfallenden Welle gestreute Welle interferiert mit der einfallenden. Aufgrund des Frequenzunterschieds bildet sich eine Schwebung, die parallel zur einfallenden Welle läuft. Diese Intensitätsmodulation mit der Frequenz nB führt über die Elektrostriktion zu einer Dichtemodulation im Medium mit einer Wellenlänge entsprechend der spontanen Schallwelle. Das wiederum führt zu einer Verstärkung der Schallwellenamplitude. Nachfolgend eintreffende Lichtwellen werden an dieser Schallwelle stimuliert gestreut [19], einfallende und gestreute Welle sind über die Schallwelle gekoppelt. Dabei wird wiederum die Schallwellenamplitude verstärkt. Die Reflektivität des Schallwellengitters und die Intensität des reflektierten Lichtes erhöht sich, die SBS wirkt als Spiegel.
Mit Hilfe der Navier-Stokes-Gleichung läßt sich die
Kopplung von Lichtwellen und Schallwelle mathematisch beschreiben.
Unter Anwendung von (2) und einigen Näherungen [6, 20]
ergeben sich drei gekoppelte Differentialgleichungen:
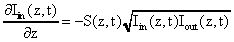 (5)
(5)
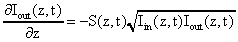 (6)
(6)
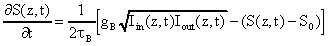 (7)
(7)Iin , Iout : Intensität der einfallenden und gestreuten Welle
S : Schallwellenamplitude
S0 : Amplitude der spontanen Schallwelle
tB : Lebensdauer der spontanen Schallwelle
z: Ort in Ausbreitungsrichtung der einfallenden Welle
gB stationärer Brillouin-Verstärkungs-Koeffizient
Aus den Gleichungen ist ersichtlich, daß der Materialparameter gB möglichst groß und tB möglichst klein gewählt werden sollte, um die Schallwelle optimal zu generieren.
Kochemasov zeigte in [21], daß die reflektierte Welle unter der Bedingung starker Fokussierung die phasenkonjugierte der Einfallenden ist. Das bedeutet, daß der Radius der Wellenfront bei der Reflexion bezüglich der Ausbreitungsrichtung umgekehrt wird.
Der Vektor des elektrischen Feldes vor der Reflexion ist gegeben
durch:
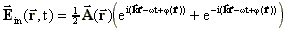 (8)
(8)
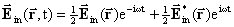 (9)
(9)Für die phasenkonjugierende Reflexion gilt unter Vernachlässigung der sehr geringen Frequenzverschiebung bei der Streuung:
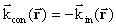 (10)
(10)
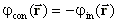 (11)
(11)
Daraus ergibt sich für die reflektierte, phasenkonjugierte
Welle:
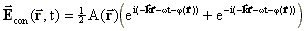 (12)
(12)
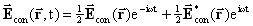 (13)
(13)Die komplexen Amplituden der einfallenden und der phasenkonjugierten Welle verhalten sich wie folgt:
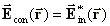 (14)
(14)Durch formales Ersetzen von t durch -t wird aus Gleichung (8) Gleichung (12). Die Phasenkonjugation verursacht ein zeitumgekehrtes Verhalten der Phasenfronten.
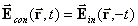 (15)
(15)Diese Eigenschaften des phasenkonjugierenden SBS-Spiegels lassen sich zur Kompensation von Phasenstörungen in Lasermedien, insbesondere in Festkörperlasermedien, ausnutzen.
Beim zweiten Durchgang des Lichtes durch ein aberrierendes Medium
nach Reflexion an einem phasenkonjugierendem Spiegel werden die
Phasenstörungen in den Phasenfronten rückgängig
gemacht (Abb. 2.1.2).
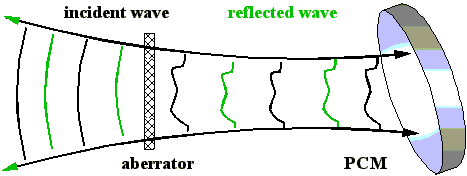
Abb. 2.1.2: Prinzipskizze eines phasenkonjugierenden
Spiegels (PCM)
Der SBS-Spiegel paßt seine Krümmung der Phasenfront des einfallenden Lichtes an, dadurch können durch den Aberrator verursachte Laufzeitunterschiede beim zweiten Durchlauf ausgeglichen werden.
Die SBS benötigt eine Startenergie bzw. -leistung, um merklich über die durch das Rauschen erzeugte spontane Brillouin-Streuung hinaus zu wachsen. Die Energie, die für eine Energiereflexion der SBS von 2% notwendig ist, wird als Schwellenergie bezeichnet.
2.2. Prinzipieller Aufbau und Funktionsweise eines SBS-Oszillators
Das hier verwendete Verfahren zur Erzeugung phasenkonjugierender Spiegel in Oszillatoren ist die SBS. Weiterführende Literatur zu Verfahren zur Erzeugung phasenkonjugierender Spiegel in Oszillatoren ist in [22 bis 30, 36] zu finden.
Der SBS-Oszillator besteht aus einem Startresonator mit der optischen
Länge Lstart und einem SBS-Resonator mit der optischen
Länge LSBS (Abb. 2.2.1). Dabei dient der Startresonator
zur Erzielung der Schwellenergien der SBS und zur Schwellabsenkung
der SBS aufgrund der longitudinalen Modenstruktur des Startresonators.
Den SBS-Resonator bilden der Auskoppelspiegel M1, das aktive Medium
(Nd:YALO) und der phasenkonjugierenden Spiegel im SBS-Medium.
Dazu ist es notwendig, im SBS Medium einen Fokus zu erzeugen,
um die Wechselwirkungslänge kleiner als die Kohärenzlänge
des Lasers zu machen. Dies kann mittels eines Teleskops im Resonator
geschehen. Dieses hat gleichzeitig den Vorteil, daß man
große Modenvolumina im aktiven Medium realisieren kann [31]
und der Stabilitätsbereich des Startresonators der Pumpleistung,
das heißt, der Änderung der thermischen Linse des aktiven
Mediums, durch Veränderung der Teleskoplänge angepaßt
werden kann. Ein Nachteil des Teleskopresonators besteht in der
Justierempfindlichkeit der Linsen. Weiterhin werden zwei Blenden
zur Selektion des TEM00 Modes und Festlegung des Arbeitspunktes
benötigt. Besonders hat sich die Ausnutzung eines Pinholes
im Fokus als erste Modenblende und Raumfilter sowie des Stabdurchmessers
als zweite Modenblende bewährt. Zur Variation der Verluste
des Startresonators werden bei kleinen mittleren Leistungen Grauglas-Filter
F verwendet bei konstantem Reflexiongrad der Spiegels M2. Bei
höheren mittleren Leistungen werden die Reflexiongrade des
Spiegels M2 variiert, da die thermischen Linsen der Graugläser
den Strahlverlauf im Resonator entscheidend verändern können.
Als SBS-Medien haben sich hochverdichtete Gase wie SF6 (2 MPa),
CO2 (5 MPa) und Xenon (5 MPa) aufgrund
ihrer geringen Absorption und hohen optischen Durchbruchsfestigkeit
bewährt.
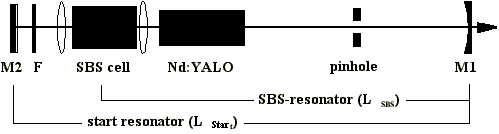
Abb. 2.2.1: Prinzipieller Aufbau eines SBS-Oszillators
Die Funktionsweise des SBS-Oszillators kann wie folgt beschrieben werden.
Nach Erreichen der Laserschwelle oszilliert das Laserlicht im
Startresonator. Das SBS-Medium ist zu dieser Zeit noch transparent,
die Verluste im Startresonator werden durch die effektiven Reflexionsgrade
der Spiegel und durch Beugungsverluste an den Blenden bestimmt.
Der exponentielle Anstieg der Intensität im ersten Spiking-Puls
des Startresonators führt dazu, daß die Schwelle der
SBS erreicht wird. Die Reflektivität des SBS-Spiegels steigt
an, das reflektierte Licht wird nach einem Umlauf im SBS-Resonator
verstärkt und erhöht damit wiederum die Reflektivität
des SBS-Spiegels. Als Folge oszilliert nur noch Licht im SBS-Resonator,
die Besetzungsinversion wird aufgrund der geringen Verluste des
SBS-Resonators in kurzer Zeit vollständig abgebaut. Die SBS
wirkt also als passiver Güteschalter [32] mit Q-switch Pulslängen
von typischerweise 20 ns bis 70 ns (FWHM). Bei hoher
Pumppulsenergie wiederholt sich dieser Güteschaltungsprozeß
innerhalb der Pumppulsdauer mehrfach. Die Folge ist ein Pulszug
(Burst) mit Pulsfolgefrequenzen im kHz-Bereich. Die Q-switch Pulslänge
Dt ist abhängig von der Lebensdauer
t der Photonen im Resonator, von der
Anfangsinversion nA, der Endinversion nE
und der Inversion nM am Intensitätsmaximum
des Q-switch Pulses [33].
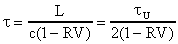 (16)
(16)
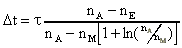 (17)
(17)R effektiver Reflexionsgrad des Resonators
V Verlustfaktor im Resonator pro Durchgang
c Vakuumlichtgeschwindigkeit
L optische Resonatorlänge
tU Umlaufzeit des Resonators
2.3. Resonatorberechnung eines Lasers mit phasenkonjugierendem SBS-Spiegel
Die Realisierung eines SBS-Oszillators mit bestmöglicher
Strahlqualität und hoher Ausgangsleistung stellt gewisse
Anforderungen an die Komponenten und Geometrie dieses Systems.
Der Gauß-Hermite-Mode TEM00 oder auch Grundmode
besitzt die physikalisch bestmögliche Strahlqualität.
Man spricht von beugungsbegrenztem Licht. Seine transversale Intensitätsverteilung
I(r) ist kreissymmetrisch und entspricht der Gauß-Verteilung:
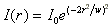 (18)
(18)
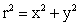 . (19)
. (19)
I0 ist die Maximalintensität und w der Strahlradius
bei I=I0 /e2 . Abb. 2.3.1 zeigt das Verhalten
der Ausbreitung eines TEM00-Strahlungsfeldes in der
Umgebung einer Strahltaille.
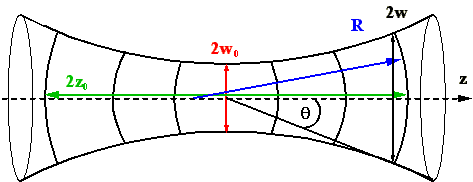
Abb. 2.3.1: Ausbreitung eines Gaußstrahls und
beschreibende Parameter
Zur Beschreibung des Gaußstrahls wird der komplexe Strahlparameter q(z) eingeführt, der den Strahlradius w (w = r aus (18)) und den Radius R der Phasenfronten an jeder Stelle z charakterisiert [17].
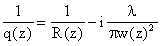 (20)
(20)l bezeichnet die Wellenlänge des Lichtes, q ist der halbe Fernfeld-Öffnungswinkel und z0 die Rayleigh-Länge mit z0=pw02/l.
Da der lineare SBS-Oszillator aus zwei Teilresonatoren besteht, die abgesehen vom kurzen Schaltprozeß zeitlich nacheinander anschwingen, können diese auch getrennt berechnet werden. Dabei greift man auf den Matrix-Formalismus zurück, bei dem jedem durchlaufenem optischen Element n des Resonators eine 2x2 Matrix Mn zugeordnet wird [17].
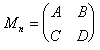 (21)
(21)Der komplexe Strahlparameter q0 vor einem Element wird durch die Matrix in den komplexen Strahlparameter q1 hinter dem Element nach dem ABCD-Gesetz (22) transformiert [17].
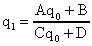 (22)
(22)
Die Matrizen der einzelnen Elemente sind der entsprechenden Literatur
zu entnehmen [17, 34, 35].
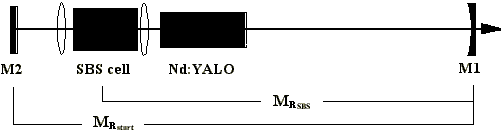
Abb. 2.2.1 Teilresonatoren und dazugehörige Umlaufmatrizen
Die Multiplikation (von links) der Matrizen aller bei einem Umlauf durchlaufener n Elemente des Startresonators führt zur Umlaufmatrix des Startresonators (23) mit m=2n-2.
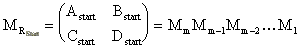 (23)
(23)Sie transformiert q0 an einer bestimmten Stelle des Resonators (üblicherweise am Auskoppler M1) in q1 an der selben Stelle. Die Stabilitätsbedingung des Resonators ist erfüllt, wenn q1= q0= qE . Das führt zur Eigenwertgleichung:
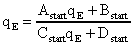 (24)
(24)
Daraus ergeben sich dann die Eigenlösungen des komplexen
Strahlparameters (25), von der nur eine physikalisch sinnvoll
ist.
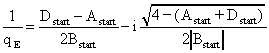 (25)
(25)Der komplexe Strahlparameter kann sich nach einem Umlauf nur mit reellem Strahlradius reproduzieren, wenn für die Komponenten der Umlaufmatrix folgende Ungleichung erfüllt ist:
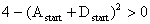

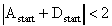 (26)
(26)Ist die Stabilitätsbedingung (26) erfüllt, so ergeben sich für den Krümmungsradius der Phasenfronten und den Strahlradius an der Startposition folgende Gleichungen:
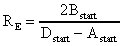
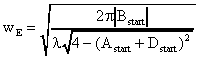 (27)
(27)
Ausgehend von der Berechnung von RE und wE
an einer Position im Resonator, kann der gesamte Strahlverlauf
im Resonator mittels des ABCD-Gesetzes bestimmt werden.
Die Berechnung der Eigenlösung des SBS-Resonators ist aufgrund der nichtlinearen Eigenschaften des SBS-Spiegels kompliziert. Giuliani stellt in [37] ein vereinfachtes Modell zur Berechnung der transversalen Moden vor. Danach kann wie folgt vorgegangen werden.
Die SBS ist ein nichtlinearen Effekt, die Reflexionseigenschaften hängen stark von der eingestrahlten Intensität ab. Die Flanken der Gaußstrahlen werden deshalb schwächer reflektiert oder bei Unterschreitung der SBS-Schwelle transmittiert. Der Strahlradius wr des reflektierten Gaußstrahls ist kleiner als der des einfallenden (wi). Dieses drückt sich im b-Faktor aus (28), der das Verhältnis beider Strahlradien am Ort zr repräsentiert (Abb. 2.2.2).
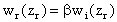 (28)
(28)Für das Verhältnis der Phasenfrontradien ergibt sich nach Kochemasov [21]:
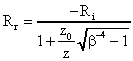 (29)
(29)Hierbei ist z die Länge des SBS-Mediums in Strahlrichtung und z0 die Rayleigh-Länge, die bei starker Fokussierung der Wechselwirkungslänge entspricht. Gleichung 29 vereinfacht sich mit z>>z0 zu:
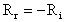 (30)
(30)
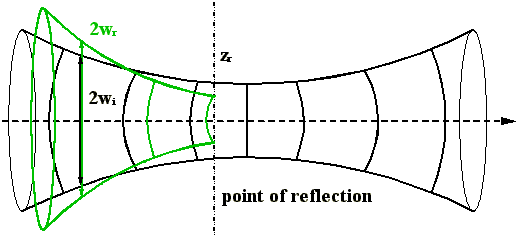
Abb. 2.2.2: Ausbreitung des einfallenden und des reflektierten
(grün) Gaußstrahls
Bei gleicher Strahlqualität führt der um b verkleinerte Strahlradius zu einer größeren Divergenz. Die Strahldivergenz des reflektierten Strahls hängt stark vom Ort der Reflexion zr ab, was sich bei der Resonatorberechnung nach Giuliani bemerkbar macht (Abb. 2.2.3).
Die Berechnung des SBS-Resonators nach [37] erfolgt mittels der
Umlaufmatrix (31) ohne die Matrix des SBS-Spiegels, die den
komplexen Strahlparameter q0 vor dem SBS-Spiegel in
den komplexen Strahlparameter q1 vor dem SBS-Spiegel
transformiert.
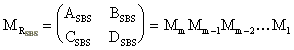 (31)
(31)
Für den von der SBS-Zelle reflektierten Strahl gelten nach
[37]:
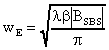
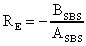 (32)
(32)Demnach bleibt der Strahlradius unabhängig von den Elementen im SBS-Resonator immer reell und endlich, der SBS-Resonator ist immer stabil.
Die Berechnungen der Resonatoren wurde mit einem von M. Ostermeyer entwickelten Programm durchgeführt.
Abb. 2.2.3 zeigt nach Giuliani errechnete Strahlverläufe
im SBS-Resonator für unterschiedliche Startpunkte der SBS.
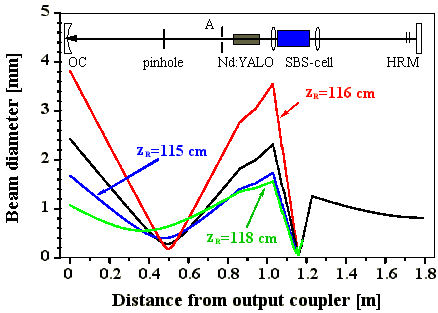
Abb. 2.2.3: Berechnete Strahlverläufe im SBS-Oszillator für verschiedene Startpunkte zr
der SBS (nach Giuliani); rot: zr in Strahltaille
des Startresonators (schwarz)
Es ist gut zu erkennen, daß die berechneten Strahlverläufe im SBS-Resonator stark variieren. Im Rahmen dieser Experimente wurde jedoch beobachtet, daß der transversale Mode des Startresonators vom SBS-Resonator übernommen wird. Deswegen sind die nachfolgenden Resonatorberechnungen nur für den Startresonator ausgeführt worden.
Weitere Modelle zur transversalen Modenstruktur von Oszillatoren mit phasenkonjugierenden Spiegeln sind in [38, 39, 40] beschrieben.
Höhere TEM-Moden können ebenfalls durch den komplexen
Strahlparameter q(z) beschrieben werden. Dabei muß beachtet
werden, daß das Strahlparameterprodukt q w0
um den Strahlausbreitungsfaktor M2 größer
ist als beim Grundmode. Das Strahlparameterprodukt aus halbem
Öffnungswinkel und Strahltaillenradius bestimmt das Verhältnis
von Fokusfläche zur Schärfentiefe eines fokussierten
Strahlungsfeldes.
M2 charakterisiert die Strahlqualität des Strahlungsfeldes.
Bei M2 =1 spricht man von beugungsbegrenztem Licht.
Der komplexe Strahlparameter [17] ergibt sich zu:
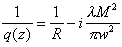 (34)
(34)2.4. Resonatorlängenabstimmung und longitudinale Moden
Bei der stimulierten Brillouin-Streuung erfährt das im Medium gestreute Licht eine Frequenzverschiebung von der Größe des Brillouin-Shifts nB. Die Idee der Resonatorlängenabstimmung liegt in der Anpassung der longitudinalen Resonatormodenabstände Dn an den Brillouin-Shift nB [14]. Dies entspricht einer Resonatorlänge, die Vielfache der Brillouin-Länge LB ist. LB ist die optische Länge, die ein Fabry-Perot-Resonator mit einem Frequenzabstand der longitudinalen Moden von nB hat (LB=c/2 nB).
Die Anpassung der Länge des Startresonators an den Brillouin-Shift
nB ist zur Schwellabsenkung
der SBS notwendig. Diese beruht auf der Existenz der zur Ursprungsfrequenz
Brillouin verschobenen Frequenz im angepaßten Startresonator.
Diese unterstützt die Brillouin Gestreute und verstärkt
den Streuprozeß erheblich (seeding). Lstart muß
demnach ganzzahliges Vielfaches der Brillouin-Länge LB
(Resonanzlänge) sein. Die im SBS-Resonator brillouinverschobenen
Frequenzen erfüllen bei SBS-Resonatorlängenanpassung
wieder die Frequenzbedingung eines Fabry-Perot-Resonators (nk=kc/2
LSBS, k=1,2,..). Die Anpassungsbedingungen lauten:
Hierbei ist c die Lichtgeschwindigkeit, m und n sind ganze Zahlen mit n m.
Bei einem Verhältnis von Lstart zu LSBS
von 2:1 wurde ein Aussetzen der SBS beobachtet und von Schumann
in [15] und Kummrow in [16] näher untersucht und beschrieben.
Dieses muß bei der Wahl der Längenverhältnisse
berücksichtigt werden. Für unterschiedliche SBS-Medien
ergeben sich entsprechende Brillouin-Längen (Resonanzlängen),
abhängig von nB . In
Tabelle 1 sind nB und
LB (37) für geeignete SBS-Medien gegenübergestellt
[18, 41, 42, 43]. Ein kleineres LB ermöglicht
eine größere Anzahl der realisierbaren Resonatorkombinationen.
Tabelle 1 LB= c/2 nB (37)
Der Schaltprozeß der SBS im Resonator führt zu einem schnellen Anwachsen der Güte im SBS-Resonator. Das gleichzeitige Auftreten mehrerer Frequenzen im SBS-Resonator führt zu Modulationen der Intensität der resultierenden Q-switch Pulse.
Die Fouriertransformierten der Intensitätsverläufe der
Pulse weisen für Maxima bei Frequenzen mit spektralem Abstand
c/2LSBS auf. Unter der Annahme, daß diese Frequenzen
Schwebungsfrequenzen longitudinaler Resonatorfrequenzen mit spektralem
Abstand c/2LSBS sind (SBS-Resonatorfrequenzen), lassen
sich die Intensitätsverläufe der Pulse aus diesen Resonatorfrequenzen
mit verschiedener Amplitude und Phasenlage wieder zusammensetzen.
Für die resultierende komplexe elektrische Feldstärke
E ergibt sich:
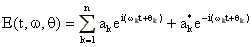 (38)
(38)Hierbei sind ak die Amplituden der einzelnen Lichtwellen, wk die Kreisfrequenzen und qk die Phasen der einzelnen Lichtwellen. Der zeitliche Intensitätsverlauf der Pulse ergibt sich aus:
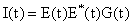 (39)
(39)G(t) ist hierbei die Gauß-Verteilung der Intensität und repräsentiert den Q-switch Puls ohne Modulation.
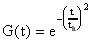 (40)
(40)th ist der 1/e-Radius der Gauß-Verteilung.
Bei der Pulsformanalyse der Q-switch Pulse des SBS-Oszillators ist zu beachten, daß sich die Resonatorfrequenzen nk aufgrund des Brillouin-Shifts ändern.
Die elektrische Feldstärke weist dann folgende Abhängigkeit
auf:
 (41)
(41)Die Änderung der Resonatorfrequenzen wird durch eine Stufenfunktion realisiert, die nach jedem SBS-Resonatorumlauf die Frequenzen um den Brillouin-Shift erniedrigt (siehe Anhang).
Die Berechnungen werden für 9 SBS-Resonatorfrequenzen durchgeführt.
Dabei wird von einer gaußförmigen Amplitudenverteilung
der Feldstärken mit SBS-Resonatorfrequenzen nk
um eine Mittenfrequenz nM
ausgegangen [44] und deren Amplitude nur leicht variiert. Der
aus (39) ermittelte Intensitätsverlauf wird einer komplexen
Fouriertransformation unterzogen. Diese Fouriertransformierten
werden mit den Fouriertransformierten der gemessenen Intensitätsverläufe
der Pulse verglichen. Die Amplitudenverhältnisse der Schwebung,
die man aus den Fouriertransformierten erhält, lassen keine
Aussage über die Amplitudenverhältnisse der Feldstärken
mit SBS-Resonatorfrequenzen zu. Die Berechnungen wurden mit dem
Programm Mathcad® 5.0 durchgeführt, eine Programmübersicht
ist im Anhang beigefügt. Die Abb. 2.5.1 bis 2.5.7 zeigen
berechnete Intensitätsverläufe der Q-switch Pulse für
unterschiedliche Parameter.
Berechnete Intensitätsverteilungen für statistische Phasenlage und konstante Amplituden, t(FWHM)=30 ns optische SBS-Resonatorlänge: 1,25 m
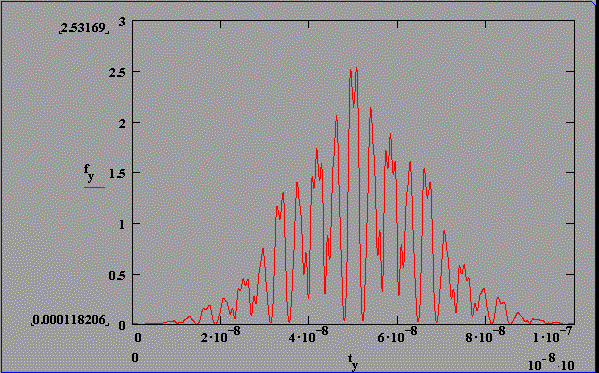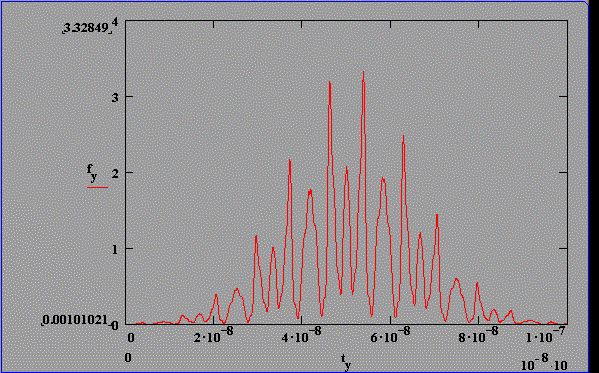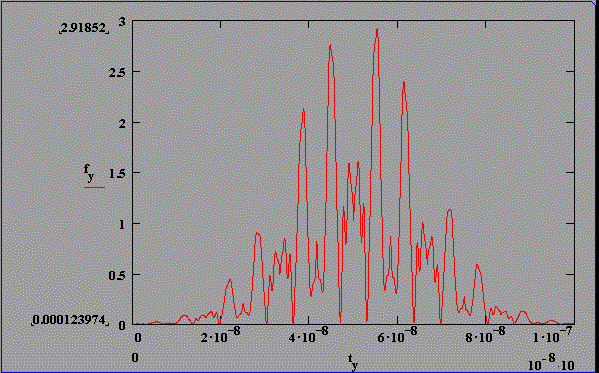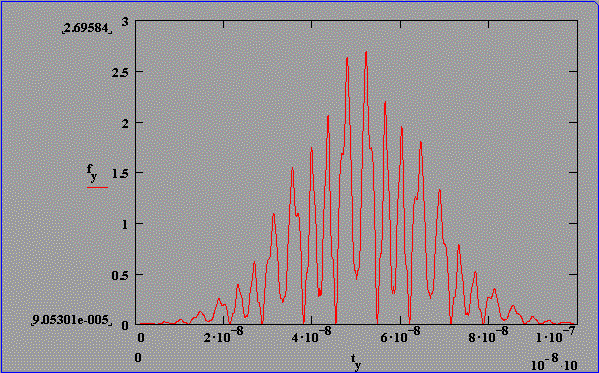
Fouriertransformierte berechneter Intensitätsverteilungen für statistische Phasenlage und konstante Amplituden, t(FWHM)=30 ns optische SBS-Resonatorlänge: 1,25 m
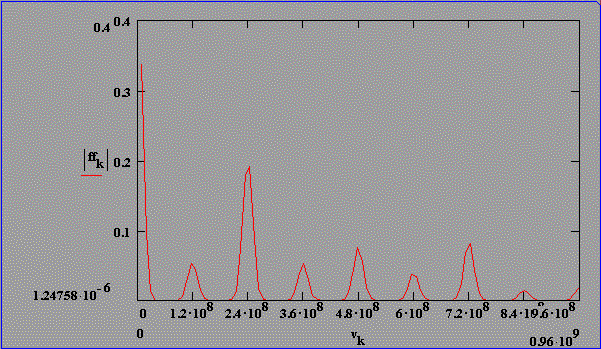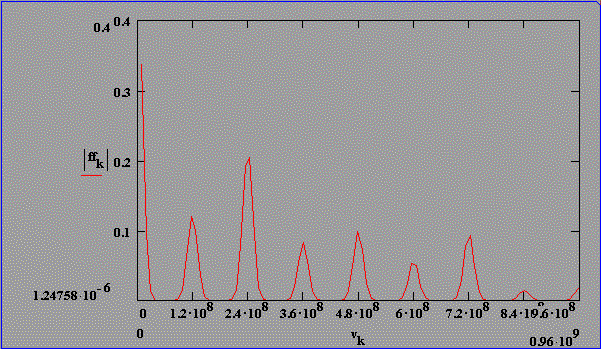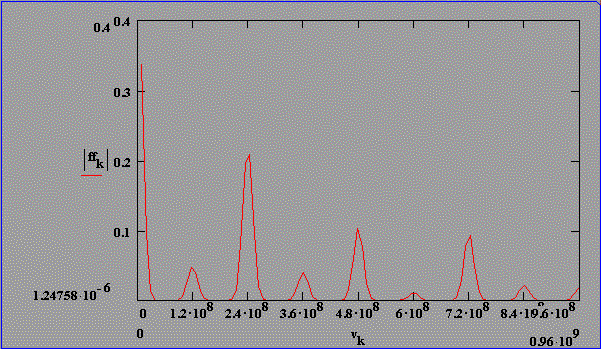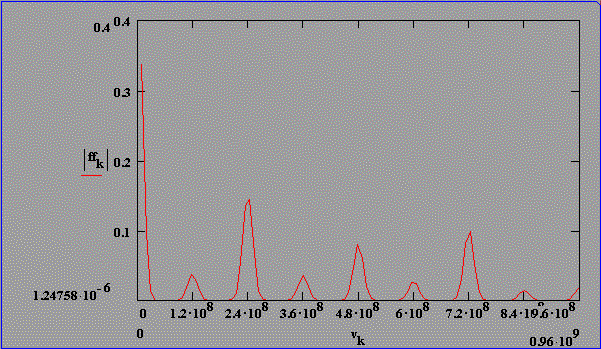
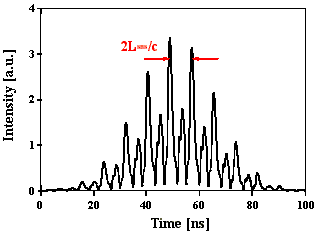
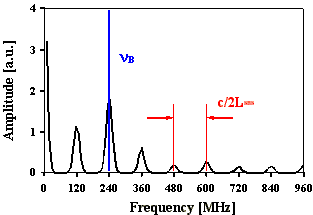
Abb. 2.5.1: Berechnete Q-switch Pulsstruktur und Fouriertransformierte für eine SBS-
Resonatorlänge von 2LB , statistischer Phase und SF6 als SBS-Medium
unter zeitlicher Berücksichtigung des Shifts
Die Amplituden der Feldstärken der SBS-Resonatorfrequenzen sind zur Vergleichbarkeit der berechneten Pulsstrukturen konstant gehalten worden. Die Pulslänge beträgt 35 ns.
Abb. 2.5.1 zeigt den Intensitätsverlauf eines Pulses mit statistischer Phasenlage der Lichtwellen unter zeitlicher Berücksichtigung des Brillouin-Shifts von SF6. Es sind deutliche Modulationsspitzen mit einem konstanten zeitlichem Abstand von 2LSBS/c (ca. 4 ns) zu erkennen, die wiederum durch eine Überstruktur von ca. 8 ns moduliert ist. Diese "Doppelstruktur" ist typisch für diese Parameterwahl. Die Fouriertransformierte des Intensitätsverlaufs weist Frequenzabstände mit c/2LSBS auf, die Amplitudenverhältnisse sind nicht äquivalent zu den Amplitudenverhältnissen der Ursprungsfrequenzen.
In Abb. 2.5.2 ist der berechnete Intensitätsverlauf
eines Pulses mit Phasenlage von 2p
dargestellt. Der Intensitätsverlauf ist aufgrund der Phasenkopplung
innerhalb einer Umlaufperiode symmetrisch. Für die Fouriertransformierte
gilt das gleiche wie für die in Abb. 2.5.1.
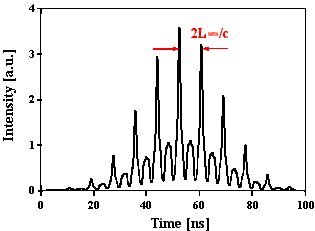
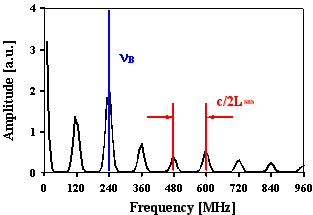
Abb. 2.5.2: Berechnete Q-switch Pulsstruktur und Fouriertransformierte für eine SBS-
Resonatorlänge von 2LB , konstanter Phase (2p) und SF6
als SBS-Medium unter zeitlicher Berücksichtigung des Shifts
Abb. 2.5.3 zeigt die berechnete Pulsstruktur und die Fouriertransformierte
für eine SBS-Resonatorlänge von 2,5*LB und
statistischer Phasenlage. Wieder sind Modulationsspitzen mit einem
konstanten zeitlichem Abstand von 2LSBS /c zu
erkennen. Die Fouriertransformierte zeigt Frequenzabstände
von 95 MHz=c/2LSBS , die Amplitudenverhältnisse
der Schwebung sind nicht äquivalent zu den Amplitudenverhältnissen
der Ursprungsfrequenzen.
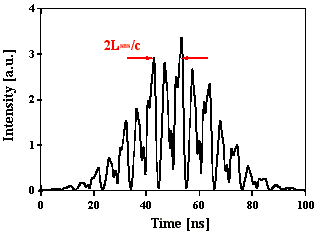
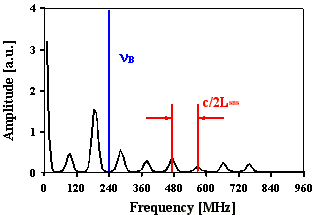
Abb. 2.5.3: Berechnete Q-switch Pulsstruktur und Fouriertransformierte für eine SBS-
Resonatorlänge von 2,5*LB , statistischer Phase und SF6 als SBS-Medium
unter zeitlicher Berücksichtigung des Shifts
Für eine SBS-Resonatorlänge von 2,5*LB und
konstanter Phasenlage (2p) weisen die
Modulationsspitzen der Pulsstruktur (Abb. 2.5.4) wieder einen
konstanten zeitlichen Abstand von 10 ns=2LSBS /c
auf. Für die Fouriertransformierte gilt das gleiche wie für
die in Abb. 2.5.3. Die Amplituden der Schwebung in den Fouriertransformierten
sind trotz konstanter Amplitude der SBS-Resonatorfrequenzen unterschiedlich.
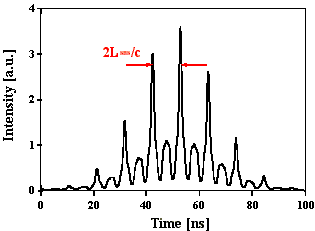
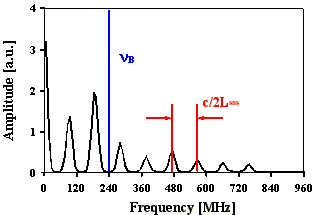
Abb. 2.5.4: Berechnete Q-switch Pulsstruktur und Fouriertransformierte für eine SBS-
Resonatorlänge von 2,5*LB , konstanter Phase (2p) und SF6
als SBS-Medium unter zeitlicher Berücksichtigung des Shifts
Abb. 2.5.5 zeigt die Pulsstruktur und die Fouriertransformierte für eine SBS-Resonatorlänge von 2,5*LB und statistischer Phasenlage ohne zeitliche Berücksichtigung des Brillouin-Shifts von SF6 .
Die Fouriertransformierten der Intensitätsverläufe weisen
mit und ohne Verringerung der Ursprungsfrequenzen um nB
nach einem SBS-Resonatorumlauf ausschließlich Frequenzabstände
mit c/2LSBS auf. Die Intensitätsverläufe
der Pulse unterscheiden sich für Berechnungen mit leicht
variierten Amplituden und statistischer Phasenlage der SBS-Resonator-frequenzen
stark, insbesondere bei nicht an die Brillouin-Länge angepaßter
SBS-Resonatorlänge. Sie weisen jedoch die typischen Strukturen
für die gewählte SBS-Resonatorlänge auf.
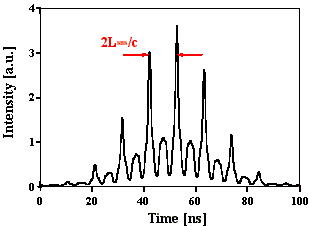
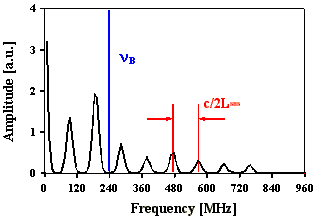
Abb. 2.5.5: Berechnete Q-switch Pulsstruktur und Fouriertransformierte für eine SBS-
Resonatorlänge von 2,5*LB , konstanter Phase (2p) und SF6
als SBS-Medium ohne zeitliche Berücksichtigung des Shifts
Fouriertransformierte berechneter Intensitätsverteilungen für statistische Phasenlage, konstante Amplituden, t(FWHM)=30 ns und optischer SBS-Resonatorlängen von 1,25 m bis 1,85 m
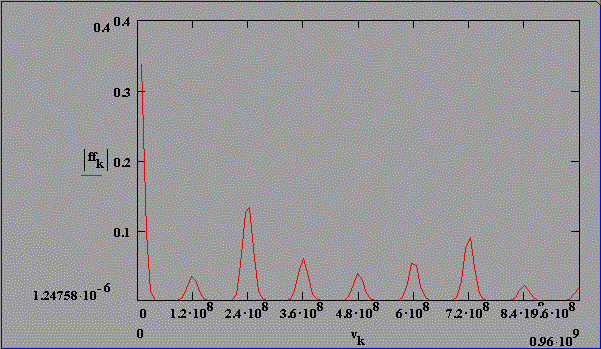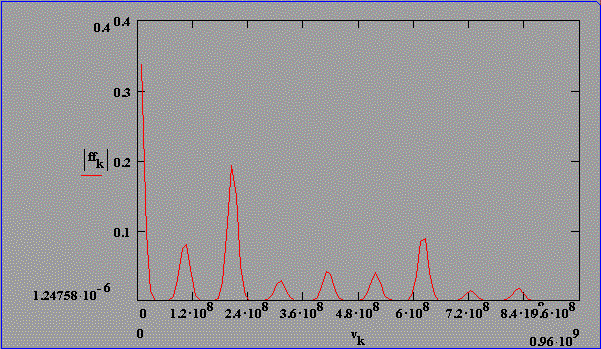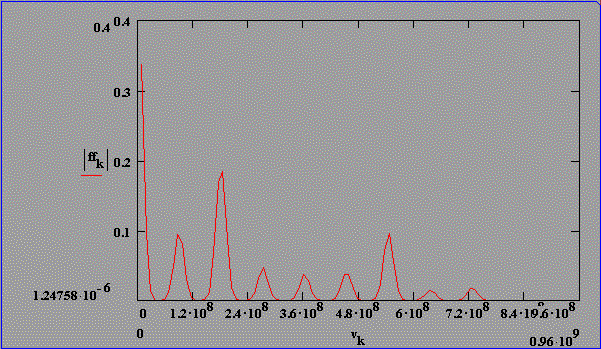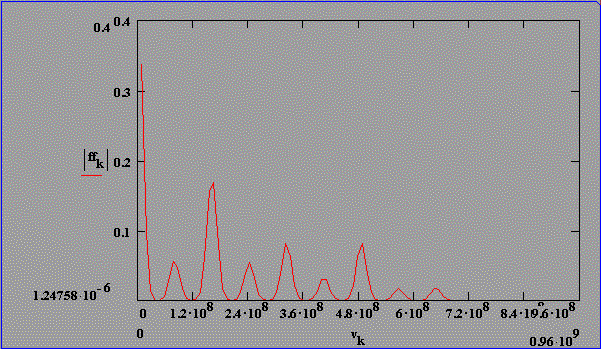
In Abb. 2.5.6 und Abb. 2.5.7 sind die Pulsstrukturen und die Fouriertransformierten für eine SBS-Resonatorlänge von 2,5*LB und statistischer Phasenlage unter zeitlicher Berücksichtigung des Brillouin-Shifts von SF6 dargestellt. Die Amplitudenverteilung ist in beiden Fällen so gewählt, daß die 4 Feldstärken mit Frequenzen nk < nM und die 4 Feldstärken mit Frequenzen nk > nM 1/10 der Amplitude der Feldstärke mit der Mittenfrequenz nM aufweisen.
Der Vergleich von Abb. 2.5.6 und Abb. 2.5.7 läßt erkennen,
daß die Amplituden der Schwebung in den Fouriertransformierten
mit der Phasenlage der Feldstärken Ek bei konstantem
Amplitudenverhältnis der Feldstärken variieren. Dieses
zeigt eindeutig, daß die Amplituden der Schwebung in den
Fouriertransformierten keine quantitative Aussage über die
Amplituden der Feldstärke des Lichts zulassen.
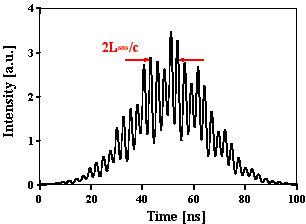
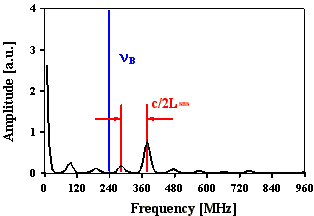
Abb. 2.5.6: Berechnete Q-switch Pulsstruktur und Fouriertransformierte für eine SBS-
Resonatorlänge von 2,5*LB , konstanter, unterschiedlicher Phase, stark
unterschiedlicher Amplituden und SF6 als SBS-Medium unter zeitlicher
Berücksichtigung des Shifts
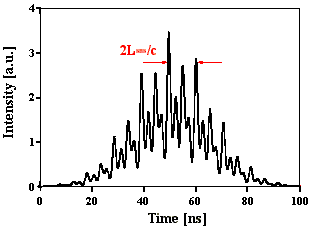
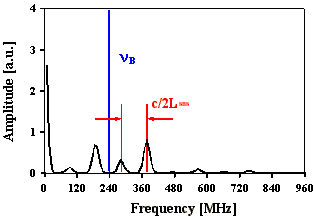
Abb. 2.5.7: Berechnete Q-switch Pulsstruktur und Fouriertransformierte für eine SBS-
Resonatorlänge von 2,5*LB , konstanter, unterschiedlicher Phase, stark
unterschiedlicher Amplituden und SF6 als SBS-Medium unter zeitlicher
Berücksichtigung des Shifts
3.1. Experimenteller Aufbau und allgemeine Meßmethoden
Die Experimente zur Abhängigkeit der longitudinalen Modenstruktur
und der Pulsenergie von den Längen des SBS-Resonators und
des Startresonators, von der Fokussierung im Teleskop sowie von
den Verlusten im Startresonator wurden mit dem in Abb. 3.1.1
dargestellten Aufbau realisiert.
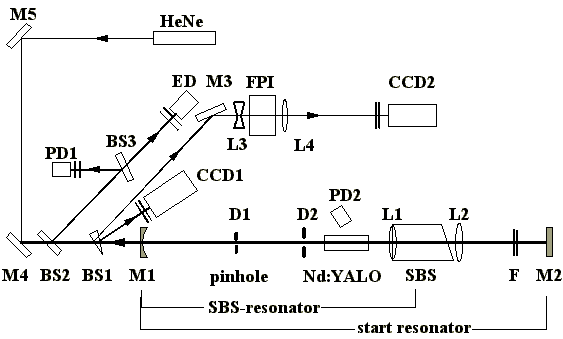
Abb. 3.1.1 Experimenteller Aufbau
M1 Auskoppelspiegel, R = 0,25 (1080 nm), r = 500 mm, 300 mm; l/10
M2 HR-Spiegel (1080 nm, 0°), plan, l/10
M3 HR-Spiegel (1080 nm, 45°), plan, l/10
M4, M5 HR-Spiegel (633 nm, 45°), plan, l/2
L1 Linse, f = 40 mm, 60 mm, 80 mm, 100 mm, 120 mm, 150 mm
L2 Linse, f = 40 mm, 40 mm, 60 mm, 80 mm, 100 mm, 120 mm
L3 Linse, f = -40 mm
L4 Linse, f = 500 mm
FPI Fabry-Perot-Interferometer, L = 40 mm, R = 0,94 beidseitig, l/50
freier Spektralbereich: 3,75 GHz, spektrale Breite: 74 MHz
SBS-Zelle Hochdruckzelle, CO2 (5,6 MPa), Xenon (5 MPa), SF6 (2 MPa)
F Graugläser (NG 12) , verschiedene Transmissionen
Nd:YALO l = 79 mm, d = 4 mm, n = 1.95 (1080 nm), 1,1 at%
thermische Linse: 3,6 dpt/kW, slope efficiency: 4,25 %
D1, pinhole Quarz-pinhole, d = 0,333 mm bis 0,447 mm, zersägte Kapillare
D2 Modenblende
BS1 BK7-Keil, 3°, polierte Seite l/10,
BS2, BS3 Quarzglas, einseitig AR-beschichtet
PD PIN-Diode, maximale Auflösung (850 nm): 840 MHz
ED pyroelektrischer Energiedetektor Gentec ED 200
CCD1, CCD2 CCD-Kameras Philips FTM 800, Auflösung (B x H) : 754x576 Pixel
6,4 mm x 4,8 mm Array
Laserkopf elliptische, abbildende Blitzlampenkavität, Eu-dotiertes Quarzglas
Oszilloskop Tektronix - Oszilloskop 684 A, 5 GS/s, analoge Bandbreite: 1 GHz
Netzteil Spektrum-Netzteil, Repetitionsrate: 3 Hz-33 Hz,
Pumppulsenergie: 12,9 J - 17,6 J, Pumppulsdauer: 140 ms
Arbeitsregime: Repetitionsrate: 20 Hz, Pumppulsenergie: 12,9 J
Der Abstand der Spiegel M1 und M2 legten die Abmessungen des Startresonators, der des Spiegels M1 und des Fokus in der SBS-Zelle den SBS-Resonator fest. Die Blenden D1 und D2 dienten der Selektion des transversalen Grundmodes und der Festlegung der jeweiligen Arbeitspunkte im Stabilitätsbereich. Die Pulsenergie, die Pulsstabilität und die longitudinale Modenstruktur sind nur dann vergleichbar, wenn für unterschiedliche Resonatorkonfigurationen die Stabilität des Startresonators, gleiche Modenvolumina und vergleichbare Arbeitspunkte desselben Stabilitätsbereichs gewährleistet sind. Unterschiedliche Stabilitätsbereiche und Arbeitspunkte führen zu abweichenden Pulsenergien und Pulsstabilitäten [15, 46, 49], die Vergleichbarkeit ist nicht mehr gewährleistet. Zur Einstellung des gewünschten Arbeitspunktes war die Linse L2 in z-Richtung beweglich, L1 war fest. Die Filter F dienten der Variation der Verluste im Startresonator. Als SBS-Zelle wurde eine Hochdruckzelle verwendet, die für Drücke bis 6 MPa ausgelegt war.
Als aktives Lasermedium diente ein Nd:YALO Stab mit einem Durchmesser von 4 mm und einer Länge von 79 mm in einer Kavität der Firma Spektrum. Der Stab war für horizontal ausgerichtete Polarisation in die Kavität eingesetzt und wurde mit einer Blitzlampe gepumpt (siehe Abb. 3.1.2 ).
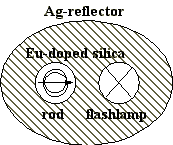
Abb. 3.1.2: Anordnung der Blitzlampe und des Stabes
in der Kavität
Das Netzteil der Firma Spektrum GmbH lieferte eine regelbare Pumppulsenergie von 12,9 J bis 17,6 J mit einer festen Pumppulsdauer von 140 ms und einer variablen Repetitionsrate von 3 Hz bis 33 Hz.. Die verwendete Kavität lieferte im Multimodebetrieb eines 60 cm-Resonators mit einem Auskoppelgrad von 50% bei 12,9 J Pumpenergie eine Ausgangsenergie von 445 mJ. Alle Experimente wurden bei 12,9 J und 20 Hz durchgeführt.
Der HeNe-Laser und die Spiegel M4 und M5 dienten zur Justage der optischen Elemente des Resonators. Über die Strahlteiler BS1, BS2, BS3 erreichte das ausgekoppelte Laserlicht die Auswerteinstrumente, die Kamera CCD1 zur Aufnahme des Strahlprofils, den Energiedetektor ED, die PIN-Diode PD1 zur Aufnahme der Zeitstruktur der Pulse. Die PIN-Diode PD2 diente zur Aufnahme des Streulichts der Blitzlampenpulse und der Q-switch Pulse. Zur Beobachtung der Frequenzen im Modenspektrum des SBS-Oszillators wurde der Strahl mittels der Linse L3 divergent gemacht und in ein Fabry-Perot-Interferometer (FPI) geschickt. Das verwendete FPI wies einen freien Spektralbereich von 3,75 GHz und eine spektrale Breite von 74 MHz auf. Die Interferenzstrukturen wurden mit der Linse L4 auf das Array der Kamera CCD2 abgebildet. Die Verluste im Resonator wurden soweit erhöht, daß nur ein Q-switch Puls während eines Blitzlampenpulses ausgebildet wurde, um Überlagerungen mehrerer Pulse während der Belichtungsdauer der Kamera CCD2 (ca. 40 ms) zu vermeiden. Das Bild der Kamera und des Oszilloskops wurde auf das Triggersignal des Pulses hin eingefroren. Dies gestattete eine eindeutige Zuordnung der FPI-Bilder zu den aufgenommenen Pulsstrukturen. Die so gewonnenen Bilder (FPI-Bilder) stellen die Aufintegration der Intensitäten aller im Puls enthalten Frequenzen dar. Aus den Ringstrukturen konnten die enthaltenen Frequenzabstände ermittelt werden.
Der Plattenabstand des verwendeten Fabry-Perot-Interferometer betrug 4 cm, der Reflexionsgrad betrug 0,94. Die Photonenlebensdauer im FPI ergibt sich aus (14) unter Annahme eines Verlustfaktors von 0.94 [34] zu 1,2 ns. Da nach einem Resonatorumlauf die Frequenz des Lichts aufgrund des Shifts verändert wird, kann im FPI nur Licht einer Frequenz interferieren, das innerhalb der Umlaufzeit des SBS-Resonators eintrifft. Dadurch wird das Auflösungsvermögen des FPIs weiter eingeschränkt.
Die Frequenzabstände 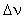 innerhalb einer
Ordnung lassen sich wie folgt berechnen [45]:
innerhalb einer
Ordnung lassen sich wie folgt berechnen [45]:
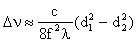 (43)
(43)Hierbei ist l die Wellenlänge des eingestrahlten Lichts, c die Vakuumlichtgeschwindigkeit und f die Brennweite der abbildenden Linse L4. Die Ringdurchmesser d wurden aus den Intensitätsprofilen der FPI-Bilder ermittelt. Die Ringabstände sind von außen nach innen durchnumeriert worden, durch Mittelung über die Anzahl der sichtbaren Abstände wurden die Frequenzabstände bestimmt.
Der Fehler bei der Ermittlung der Ringdurchmesser betrug 16 mm,
der doppelte Pixelabstand des Kamera-Arrays. Der Fehler der Linsenbrennweite
wurde vom Hersteller mit 2% angegeben. Beide Fehler gehen quadratisch
in 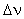 ein. Daraus ergibt sich ein relativer
Fehler für
ein. Daraus ergibt sich ein relativer
Fehler für 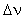 von weniger als 5%
für Ringabstände mit Ringradien kleiner 2,4 mm.
Das spektrale Auflösungsvermögen des FPIs betrug 74 MHz.
von weniger als 5%
für Ringabstände mit Ringradien kleiner 2,4 mm.
Das spektrale Auflösungsvermögen des FPIs betrug 74 MHz.
Alle Pulslängen sind über einen Gauß-Fit mit dem Programm ORIGIN® ermittelt worden und in FWHM angegeben.
Die Pulsstabilität ist als Standardabweichung (+-) eines Histogramms über 500 Blitzlampenpulse angegeben.
Die Frequenzen in den Fouriertransformierten sind mit einem relativen
Fehler kleiner 5% behaftet. Dieser resultiert aus der digitalen
Abtastrate des Oszilloskops.
3.1.1 Variation der SBS-Resonatorlänge
Zur Untersuchung der Einflüsse der Längenabstimmung des SBS-Resonators wurde ein Resonator mit SF6 (2 MPa) als SBS-Medium mit einer Anpassung an die Brillouin-Länge von 2:3 (SBS-Resonatorlänge:Startresonatorlänge) als Ausgangskonfiguration gewählt. Die Startresonatorlänge wurde konstant gehalten, der SBS-Resonator wurde in Schritten von 2.5 cm verlängert (Abb. 3.1.3) und damit maximal außer Resonanz gebracht, so daß das Frequenzmaximum des geshifteten Lichtes in ein Minimum der Airy-Formel eines Fabry-Perot-Resonators mit SBS-Resonatorlänge fällt (rote Kurve in Abb. 3.1.4). Dabei ist auf die Stabilität der Resonatoren, auf vergleichbare Arbeitspunkte (Abb. 3.1.5) und auf gleiche Modenvolumina geachtet worden. Dazu wurde die Resonatorkonfiguration derart gewählt, daß der berechnete Strahlverlauf durch das Pinhole und den Stabdurchmesser für alle SBS-Resonatorlängen begrenzt ist. Jede Abweichung vom berechneten Strahlverlauf hat erhöhte Verluste zur Folge, so daß nur auf maximale Burstenergie bei gleichzeitig geringstem Pulsabstand justiert werden mußte. Die Linse L1 wurde mit der SBS-Zelle verschoben, mit der Linse L2 wurde der Arbeitspunkt eingestellt (Abb. 3.1.5). Für Resonatorlängenabstände von 10 cm wurden jeweils drei zeitliche Pulsverläufe mit den dazu gehörenden FPI-Bildern, ein Strahlprofil und für alle Resonatorlängen jeweils ein Histogramm der Puls-energien über 500 Blitzlampenpulse aufgenommen. Die spezifizierten Brennweiten der Teleskoplinsen betrugen L1=60 mm, L2=40 mm, der Pinholedurchmesser betrug 0,432 mm.
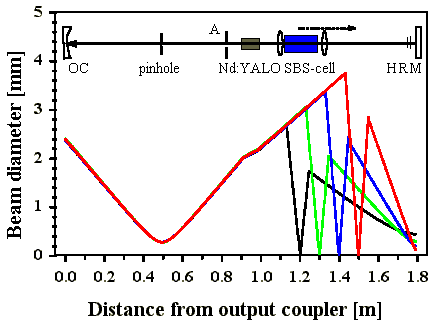
Abb 3.1.3: Berechnete Strahlverläufe im Startresonator für verschiedene
SBS-Resonatorlängen (SF6)
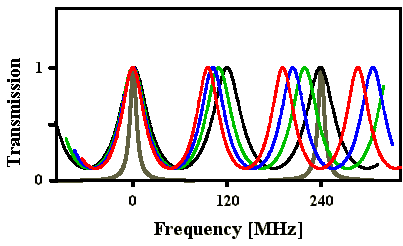
Abb. 3.1.4: Brillouin-Shift von SF6 (grau) und spektrale Resonatormodenabstände
für die SBS-Resonatorlängen aus Abb. 3.1.3
(Airy-Formel unter Annahme einer Modenbreite von 40 MHz)
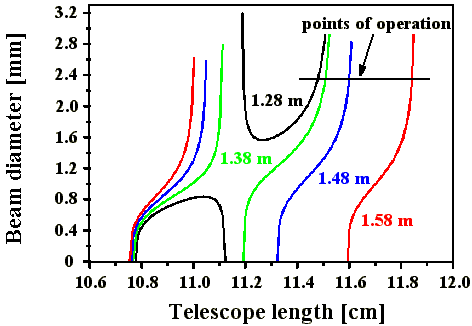
Abb. 3.1.5: Berechnete Stabilitätsbereiche (SF6) des Startresonators für die SBS-
Resonatorlängen aus Abb. 3.1.3 (Strahldurchmesser am Auskoppler)
3.1.2 Variation der Startresonatorlänge
Die Variation der Startresonatorlänge wurde mit SF6, Xenon und CO2 als SBS-Medien durchgeführt. Die Resonatoren wurden wieder nach den Kriterien der Stabilität des Startresonators, vergleichbarer Arbeitspunkte und gleicher Modenvolumina (siehe Abb. 3.1.6 und Abb. 3.1.7) berechnet und aufgebaut.
Zur Untersuchung der longitudinalen Modenstruktur wurde SF6
als SBS-Medium verwendet. Die Ausgangslängenabstimmung auf
die Brillouin-Länge betrug 2LB (SBS-Resonator)
und 3LB (Startresonator). Die verwendeten Teleskoplinsen
waren mit 60 mm (L1) und 40 mm (L2) Brennweite
spezifiziert. Der Startresonator wurde von 3LB-20 cm
bis 3LB+20 cm in Schritten von 10 cm
variiert. Dazu wurde jeweils ein Histogramm der Pulsenergien
über 500 Pulse und zwei Pulse mit den dazu gehörenden
FPI-Bildern aufgenommen. Desweiteren ist der Startresonator
mit SF6 in 5 cm-Schritten von 3LB-15 cm
bis 4LB+10 cm (Abb. 3.1.8) verlängert
worden. Dazu wurde jeweils einem Histogramm der Pulsenergie über
500 Pulse aufgenommen.
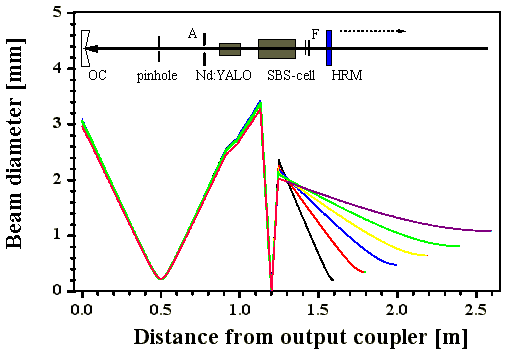
Abb. 3.1.6: Berechnete Strahlverläufe im Resonator (SF6) für verschiedene
Startresonatorlängen
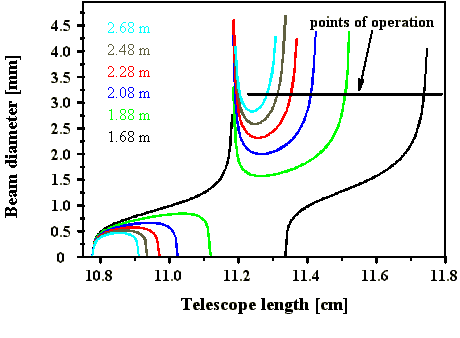
Abb. 3.1.7: Berechnete Stabilitätsbereiche für die Startresonatorlängen (SF6) aus
Abb. 3.1.6 (Strahldurchmesser am Auskoppelspiegel)
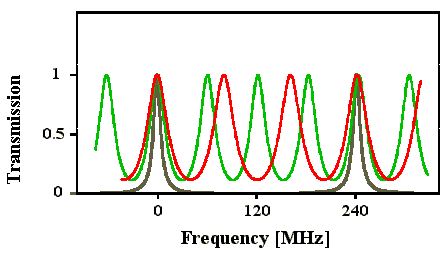
Abb. 3.1.8: Brillouin-Shift für SF6 (grau) und spektrale Startresonatormodenabstände
für resonante Startresonatorlängen
(Airy-Formel unter Annahme einer Modenbreite von 40 MHz)
Für alle drei SBS-Medien wurde weiterhin der Startresonator von einer Resonanz zur nächsten verlängert. Für SF6 und Xenon wurde der Startresonator von der dreifachen zur vierfachen Resonanzlänge in Schritten von 5 cm mit LSBS=2LB verlängert Die Teleskop-linsen hatten für Xenon Brennweiten von 150 mm (L1)und 120 mm (L2).
Für CO2 wurde der Startresonator von der
vierfachen zur fünffachen Resonanzlänge in Schritten
von 5 cm bei einer SBS-Resonatorlänge von 3LB
verlängert. Die Teleskoplinsen hatten Brennweiten von 120 mm (L1)
und 80 mm (L2). Für alle Startresonatorlängen
wurde ein Histogramm der Burstenergien über 500 Blitzlampenpulse
aufgenommen.
3.1.3. Variation der Verluste im Startresonator
Die Variation der Verluste im Startresonator wurde mit SF6, Xenon und CO2 als SBS-Medien durchgeführt. Der Startresonator und der SBS-Resonator waren auf die jeweilige Brillouin-Länge LB abgestimmt mit einem Verhältnis von 3:2 (Startresonator zu SBS-Resonator) für SF6 und Xenon beziehungsweise 4:3 für CO2 . Die Konfiguration der Teleskoplinsen war gleich denen der Variation des Startresonators. Der effektive Reflexionsgrad von M2 wurde mit den Filtern F in Stufen der Transmission der Graugläser (NG12) von (0,84)2 erniedrigt (RM2 =0,842n, n=0...8). Die verwendeten Graugläser erzeugen einen Strahlversatz und einen Keil, bei höheren mittleren Leistungen eine thermische Linse. Deswegen wurde bei kleinen mittleren Leistungen gearbeitet, der Keil wurde durch Nachjustage des Startresonatorspiegels ausgeglichen.
Für alle 3 Medien und für die verschiedenen Verluste
im Startresonator wurde jeweils ein Histogramm über
500 Blitzlampenpulse, ein zeitlicher Pulsverlauf und ein
Blitzlampenpuls mit Q-switch Pulsen aufgenommen und ausgewertet.
3.1.4. Variation der Fokussierung in der SBS-Zelle
Zur Untersuchung der longitudinalen Modenstruktur in Abhängigkeit von der Fokussierung im Teleskop wurden Resonatoren mit SF6 (2 MPa) als SBS-Medium mit einer Längenanpassung an die Brillouin-Länge von 2:3 (SBS-Resonatorlänge zu Startresonatorlänge) gewählt. Wieder wurden die Resonatoren nach den Kriterien der Stabilität des Startresonators, vergleichbarer Arbeitspunkte und gleicher Modenvolumina (siehe Abb. 3.1.9 und Abb. 3.1.10) berechnet und aufgebaut.
Für die verschiedenen Teleskopkonfigurationen wurden jeweils drei Pulsverläufe mit den dazu gehörenden FPI-Bildern und jeweils ein Histogramm der Pulsenergien über 500 Pulse aufgenommen. Es wurden folgende Teleskopkonfigurationen verwendet:
f1 = 40 mm : f2 = 40 mm,
f1 = 60 mm : f2 = 40 mm,
f1 = 80 mm : f2 = 60 mm,
f1 = 100 mm : f2 = 80 mm,
der Pinholedurchmesser betrug 0,432 mm.
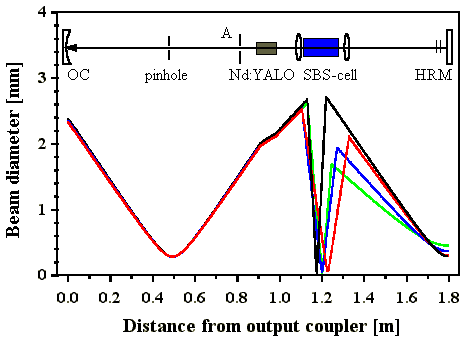
Abb. 3.1.9: Berechnete Strahlverläufe im Resonator (SF6) für die realisierten
Teleskopkonfigurationen
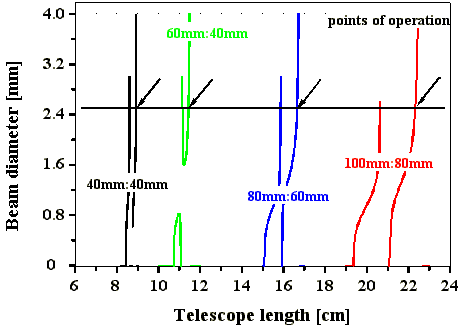
Abb. 3.1.10: Berechnete Stabilitätsbereiche (SF6) für die realisierten Teleskopresonatoren
(Strahldurchmesser am Auskoppelspiegel)
3.2. Untersuchungen zur Phasenkonjugation
im SBS-Oszillator
Zur Untersuchung der phasenkonjugierenden Eigenschaften der SBS
im Resonator in Abhängigkeit von der Stärke der Aberrationen
und von den Verlusten im Startresonator wurden der folgende Aufbau
realisiert (siehe Abb. 3.2.1).
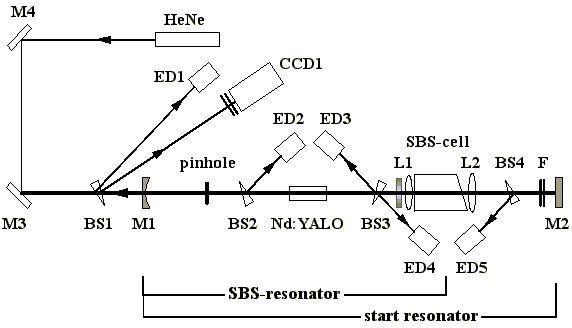
Abb. 3.2.1: Experimenteller Aufbau zur Untersuchung der Phasenkonjugation mit SF6
als SBS-Medium
M1 Auskoppelspiegel, R = 0,25 (1080 nm), r = 300 mm, l/10
M2 HR-Spiegel (1080 nm, 0°), plan, l/10
M3, M4 HR-Spiegel (633 nm, 45°), plan, l/2
L1 Linse, f = 103 mm (1064 nm)
L2 Linse, f = 83 mm (1064 nm)
SBS - Zelle Hochdruckzelle, SF6 (2 MPa), n = 1,02 (1064 nm)
F Graugläser (NG12), verschiedene Transmissionen
Nd:YALO l = 79 mm; d = 4 mm; n = 1.95 (1080 nm); 1,1 at%
thermische Linse: 3,8 dpt/kW
pinhole Quarz-pinhole, d = 0,442 mm
BS1, BS4 BK7-Keil; 3° ; n=1,51 ; R(0°)=4,12%; polierte Seite l/10,
BS2, BS3 Quarzkeil, 1° ; n=1,45 ; R(0°)=3,37%; polierte Seite l/10,
PD PIN-Diode, max. Auflösung (850 nm) : 840 MHz
ED1....ED5 pyroelektrischer Energiedetektor Gentec ED 200
CCD1 CCD-Kamera Philips FTM 800, Auflösung (B x H) : 754x576 Pixel,
6,4mm x 4,8mm
Laserkopf elliptische, abbildende Blitzlampenkavität, Eu-dotierte flow tubes
Oszilloskop Tektronix - Oszilloskop 684 A, 5 GS/s, analoge Bandbreite: 1 GHz
Netzteil Baasel
Arbeitsregime: Repetitionsrate: 20 Hz, Pumppulslänge: 0,5 ms, mittlere
Pumpleistung: 350 W, Pinhole: 0,442 mm
Der Startresonator und der SBS-Resonator waren mit einem Verhältnis
von 3:2 (Startresonator zu SBS-Resonator) auf die Brillouin-Länge
LB abgestimmt . Der effektive Reflexionsgrad von M2
wurde mit den Filtern F in Stufen der Transmission der Graugläser
(NG 12) von (0,84)2 erniedrigt (RM2 =0,842n,
n=0...8). Dies geschah einmal mit Aberrator im SBS-Resonator
und einmal ohne. Als Aberrator diente eine transparente
Petrischale, die zuvor bezüglich ihrer Phasenstörungen
untersucht wurde. Diese wurde zwischen der Kavität und der
SBS-Zelle vor der Teleskoplinse L1 plaziert. Dazu wurden jeweils
die Burstenergien an den Energiedetektoren ED1 bis ED5
über 10 Blitzlampenpulse gemittelt aufgenommen:
ED1 Ausgangsenergie Eout
ED2 Energie in Richtung Pinhole Epin
ED3 Energie in die Zelle Einc
ED4 Energie von der Zelle Eref
ED5 transmittierte Energie Etrans
Der Energiereflexionsgrad RESBS
der SBS ergibt sich aus:
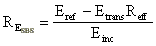 (44)
(44)Reff ist der effektive Reflexionsgrad des Startresonatorspiegels M2. Hierbei wird angenommen, daß das durch die SBS-Zelle transmittierte Licht am Startresonatorspiegel reflektiert und aufgrund seiner geringen Intensität ungehindert durch die Zelle transmittiert wird.
Die Transmission T der Zelle ergibt sich aus:
Die Verluste 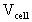 durch die Zelle ergeben
sich zu:
durch die Zelle ergeben
sich zu:
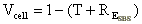 (46)
(46)
Zur Berechnung der Energieverluste Vpin am Pinhole
wurde folgende Gleichung verwendet:
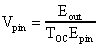 (47)
(47)
Hierbei ist TOC die Transmission des Auskoppelspiegels
M1.
Zur Aufnahme der zeitlichen Struktur der Pulse sind die
Energiedetektoren ED3 und ED4 durch PIN-Dioden ersetzt worden.
Mit einem Oszilloskop wurden die über 10 Pulse gemittelten
Pulsstrukturen aufgenommen und ausgewertet. Die Intensitäten
der Pulse wurden über die Energien normiert. Dazu wurde mit
dem Programm ORIGIN® über die Intensitätsverläufe
integriert und die Integralverhältnisse den Energieverhältnissen
gleichgesetzt. Durch Quotientenbildung des reflektierten und des
einfallenden Intensitätsverlaufs ergibt sich der zeitabhängige
Leistungsreflexionsgrad. Dieser Verlauf wurde zur Abschwächung
der Modulationen über 50 Punkte (10 ns) geglättet.
Zur Bestimmung der zeitabhängigen Verluste am Pinhole
wurden die zeitlichen Strukturen des ausgekoppelten Laserlichtes
und des am Pinhole gestreuten Lichts mit einer Photodiode
detektiert (nacheinander über 10 Blitzlampenpulse gemittelt),
um Abweichungen durch unterschiedliche Zeitkonstanten der Dioden
zu vermeiden. Das Streulicht des Pinholes wurde auf die Diode
abgebildet. Die Intensitätsverläufe wurden über
die Energien normiert. Die Zeitabhängigkeit der Verluste
am Pinhole läßt Rückschlüsse auf die Qualität
der Phasenkonjugation zu.
4.1. Variation der SBS-Resonatorlänge mit SF6 als SBS-Medium
4.1.1. Auswirkungen auf die Pulsenergie und Pulsstabilität
Die Änderung der SBS-Resonatorlänge (siehe Kap. 3.1.1) hatte keine signifikante Änderung der Pulsenergie und der Pulsstabilität zur Folge (Abb. 4.1.1). Die Energien im Pulszug (Burst) variierten zwischen 90 mJ und 120 mJ bei 4 bis 6 Pulsen im Burst. Die Pulse wiesen Energien von 20 mJ 5 mJ bei Pulslängen (FWHM) von 40 ns bis 60 ns auf. Die Standardabweichung der Burstenergie variierte zwischen 2 % und 5 %. Der effektive Re-flexionsgrad des Startresonatorspiegels M2 betrug etwa 38 %. Die Abweichungen der Pulsenergien sind durch unvermeidbare Justierungenauigkeiten zu erklären, da der SBS-Oszillator nach jeder Verschiebung der SBS-Zelle mit Teleskop neu aufgebaut wurde.
Aus diesem Ergebnis folgt, daß die Längenanpassung
des SBS-Resonators an die Brillouin-Länge zur Gewährleistung
der Stabilität der Pulsenergien nicht notwendig ist.
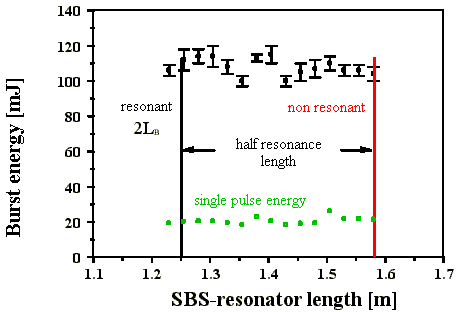
Abb. 4.1.1: Burstenergien in Abhängigkeit von der SBS-Resonatorlänge
mit SF6 als SBS-Medium
4.1.2. Transientes Modenverhalten
Interferenzstrukturen des FPI auf der CCD-Camera bei einer Repetitionsrate von 20 Hz.

Die Auswertung der Ringstrukturen der Bilder des Fabry-Perot-Interferometers
für einen Q-switch Puls läßt nur Frequenzabstände
erkennen, die dem Brillouin-Shift des verwendeten SBS-Mediums
entsprechen (Abb. 4.1.2 und Abb. 4.1.5), vereinzelt
auch Frequenzabstände der Startresonatormoden und die Differenzen
beider (Abb. 4.1.3), unabhängig von der SBS-Resonatorlänge
(Abb. 4.1.4).

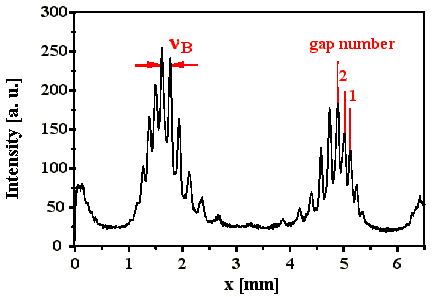
Abb. 4.1.2: FPI-Bild und dazugehöriger Schnitt bei einer SBS-Resonatorlänge von 2.5*LB
mit SF6 als SBS-Medium

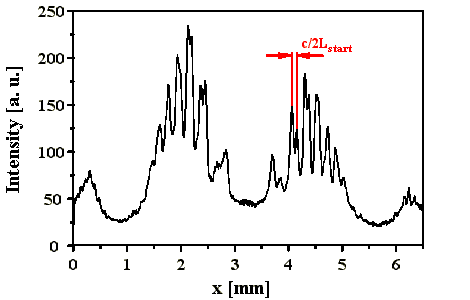
Abb. 4.1.3: FPI-Bild und dazugehöriger Schnitt bei einer SBS-Resonatorlänge von 2.5*LB
mit SF6 als SBS-Medium
In Abb. 4.1.4 sind die aus den FPI-Bildern ermittelten Frequenzabstände
(pro Bild über alle sichtbaren Frequenzabstände gemittelt)
über der SBS-Resonatorlänge aufgetragen, in Abb. 4.1.5
für die SBS-Medien CO2 und Xenon über der
Nummer der Ringabstände (siehe Abb. 4.1.2). Die Ringabstände
sind von außen nach innen ausgezählt, entsprechend
dem zeitlichen Verhalten der auftretenden Frequenzen. Innere Ringe
entsprechen kleineren Frequenzen und erscheinen deshalb später
[47].
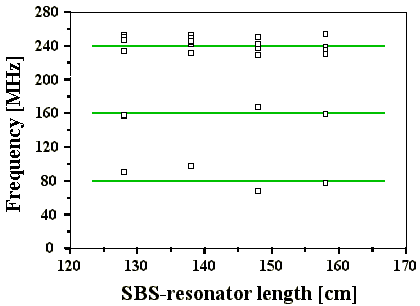
Abb. 4.1.4: Aus den FPI-Bildern ermittelte Frequenzabstände mit SF6 als SBS-Medium
in Abhängigkeit der SBS-Resonatorlänge
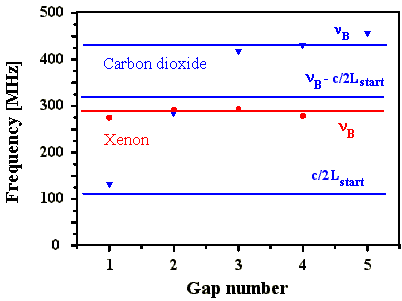
Abb. 4.1.5: Aus den FPI-Bildern ermittelte Frequenzabstände mit Xenon und
CO2 als SBS-Medien
4.1.3. Auswirkungen auf die Zeitstruktur der Pulse
Die Fouriertransformierten der Intensitätsverläufe der
Pulse zeigen ausschließlich Frequenzabstände,
die den SBS-Resonatorfrequenzabständen c/2LSBS
entsprechen (Abb. 4.1.6 bis 4.1.8). Bei guter Anpassung
der SBS-Resonatorlänge und der Startresonatorlänge an
die Brillouin-Länge sind die Pulse stark durchmoduliert,
häufig mit zeitlichen Abständen der Modulationsspitzen,
die der Umlaufzeit eines Resonators mit der Brillouin-Länge
LB entsprechen (Abb. 4.1.6).
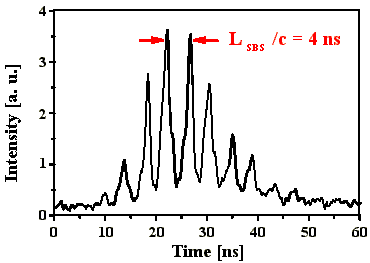
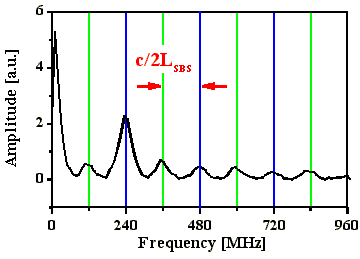
Abb. 4.1.6: Q-switch Puls und dessen Fouriertransformierte bei einer SBS-
Resonatorlänge von 2LB mit SF6 als SBS-Medium
(blaue Linien entsprechen Frequenzabständen nB
)
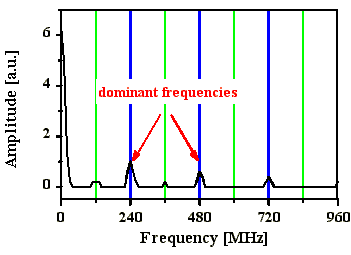
Abb. 4.1.7: Über 10 Pulse gemittelte Fouriertransformierte bei einer SBS-Resonatorlänge
von 2LB mit SF6 als SBS-Medium
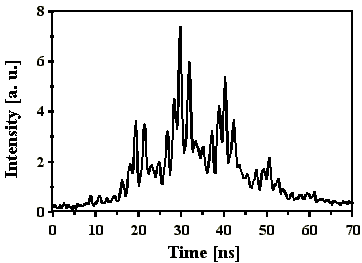
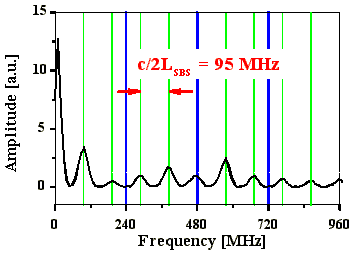
Abb. 4.1.8: Q-switch Puls und dessen Fouriertransformierte bei einer SBS-
Resonatorlänge von 2,5*LB mit SF6
als SBS-Medium
Die in Abb. 4.1.6 und 4.1.8 dargestellten Intensitätsverläufe der Pulse können mit dem in Kapitel 2.5. vorgestellten Verfahren in sehr guter Übereinstimmung reproduziert werden.
Unter der Annahme statistischer Phasenlage und variabler Amplitude der Feldstärken mit Frequenzen spektralen Abstands c/2LSBS ergeben sich für unterschiedliche SBS-Resonatorlängen die typischen Pulsstrukturen. Auch die statistische Schwankung der Modulationen ist denen der Q-switch Pulse sehr ähnlich. Die Ursache der Modulation der Q-switch Pulse sind mit großer Wahrscheinlichkeit SBS-Resonatorfrequenzen.
In Abb. 4.1.9 ist ein berechneter Intensitätsverlauf für
eine SBS-Resonatorlänge von 1,58 m dargestellt. Der
Vergleich mit Abb. 4.1.8 zeigt, daß die Intensitätsverläufe
und Fouriertransformierten sehr ähnlich sind. Die Modulationen
im gemessenen Intensitätsverlauf sind schwächer als
im Berechneten, da die SBS-Resonatorfrequenzen eine gewisse spektrale
Breite aufweisen. Diese wurde bei der Berechnung nicht berücksichtigt.
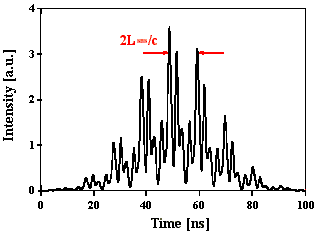
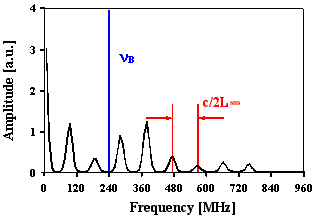
Abb. 4.1.9: Berechnete Q-switch Pulsstruktur und Fouriertransformierte für eine SBS-
Resonatorlänge von 2,5*LB , statistischer Phase und SF6 als SBS-Medium
unter zeitlicher Berücksichtigung des Shifts
In Abb. 4.1.10 sind die über die Anzahl der erkennbaren spektralen
Abstände in den Fouriertransformierten der Pulsstrukturen
gemittelten Frequenzabstände über der SBS-Resonatorlänge
aufgetragen. Die Abweichungen von der errechneten Hyperbel c/2LSBS
liegen innerhalb des Meßfehlers. Der relative Fehler für
die Frequenzen ist kleiner 5%. Dieser Fehler ergibt sich aus der
digitalen Abtastrate des Oszilloskops. Durch Mittelung über
mehrere spektrale Abstände läßt sich der Fehler
reduzieren.
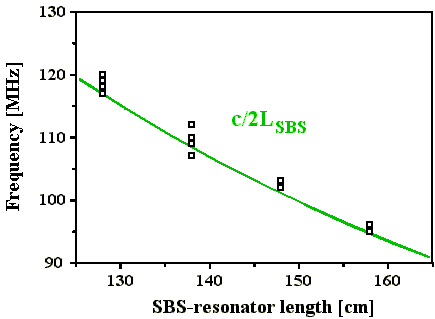
Abb. 4.1.10: Aus den Fouriertransformierten ermittelte Frequenzabstände mit SF6
als SBS-Medium in Abhängigkeit von der SBS-Resonatorlänge
In Abb. 4.1.11 sind die Intensitätsverläufe eines
Pulses abgebildet, der eine hinter dem Auskoppler M1 aufgenommen
(blau), der andere hinter dem Startresonatorspiegel M2 (grün).
Beide Pulse sind mit unterschiedlicher Intensitätsabschwächung
aufgenommen und dargestellt. Der Intensitätsverlauf des hinter
dem Startresonatorspiegel aufgenommenen Pulses (grün) zeigt
in den ersten 200 ns einen flachen Anstieg, bis der Güteschaltungsprozeß
einsetzt (200 ns-350 ns). In der Fouriertransformierten
des Intensitätsverlaufs der ersten 150 ns der vorderen
Flanke (grün) sind Frequenzabstände c/2Lstart
zu erkennen. Die Fouriertransformierte des Intensitätsverlaufs
von 200 ns bis 350 ns läßt Frequenzabstände
mit c/2LSBS erkennen. Der Güteschaltungsprozeß
startet aus dem ersten Spike des Startresonators heraus.
Eine Verschiebung des Einsatzzeitpunktes der Güteschaltung
innerhalb der Spike-Flanke in Abhängigkeit von der SBS-Resonatorlänge
war nicht erkennbar.
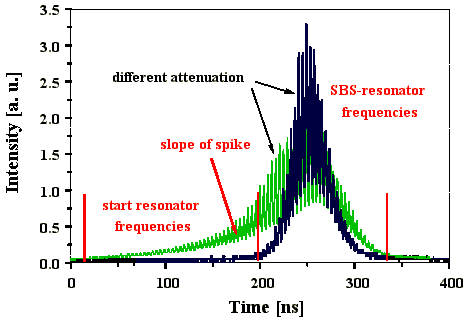
Abb. 4.1.11: Q-switch Puls (gemittelt über 10 Pulse) hinter dem Auskoppler M1 (blau)
und hinter dem Startresonatorspiegel M2 (grün) mit SF6
als SBS-Medium
4.2. Variation der Startresonatorlänge mit SF6, CO2 und Xenon als SBS-Medien
4.2.1. Auswirkungen auf die Pulsenergie und Pulsstabilität
Die Güteschaltung durch die SBS wird nur in der
Umgebung der Vielfachen der Brillouin-Länge (LB=c/2nB)
beobachtet, für SF6 3LB 15 cm
, für CO2 4LB 10 cm und für
Xenon 3LB 10 cm. Bei stärkerer Längenverstimmung
oszilliert nur Licht im Startresonator entsprechend geringer Güte
im Spiking (Abb. 4.2.1). Die Breite dieser Umgebung wird
durch die Linienbreite des SBS-Mediums und durch die spektrale
Breite der Startresonatormoden bestimmt, sie bildet ein Plateau
mit steil abfallenden Flanken. Die Pulsstabilität bleibt
durch die leichte Verstimmung im Rahmen der Meßgenauigkeit
unbeeinflußt. Bei einem Verhältnis von SBS-Resonator
zu Startresonator von 1:2 erfolgt ebenfalls keine Güteschaltung,
der Startresonator bildet Spiking Pulse. Die Breite dieses Bereiches
beträgt (21) cm. Dieser Effekt wurde schon von Schumann
in [15] beschrieben und erklärt. Die Längenanpassung
des Startresonators an LB ist zur Gewährleistung
der Stabilität der Pulsenergien des SBS-Oszillators unbedingt
notwendig.
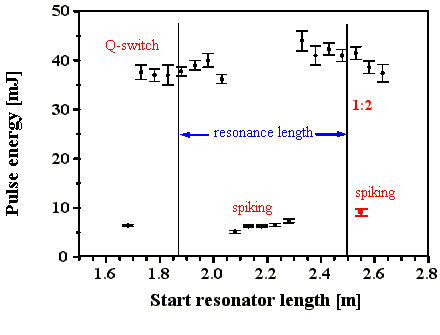
Abb. 4.2.1: Pulsenergien und Pulsstabilitäten des Lasers (SF6) in Abhängigkeit von der
Startresonatorlänge
Die Meßergebnisse können wie folgt interpretiert werden. Ohne die an nB (innerhalb der Linienbreite) angepaßte longitudinale Modenstruktur im Startresonator kommt es nicht zur Schwellherabsetzung der SBS (siehe Kap 2.4.). Das SBS-Medium bleibt unabhängig von der Pumpleistung transparent, da die Energie der Spiking Pulse die Schwellenergie der SBS nicht erreicht. Die Energie des ersten Spikes wird durch seinen Einsatzzeitpunkt und damit durch die Verluste im Startresonator bestimmt.
Die ausgekoppelten Burstenergien der SBS-Oszillatoren der verschiedenen SBS-Medien in Abhängigkeit von der Startresonatorlänge zeigen das gleiche Verhalten. Die Güteschaltung durch die SBS ist für alle Medien nur in der Umgebung der Resonanzstellen zu beobachten (Abb. 4.2.2). Die scheinbare Glockenkurve um die Resonanzstellen herum entsteht durch Mittelung, da sich an den Grenzen zum Spiking eine schwankende Anzahl von Q-switch Pulsen im Burst bildet. Die unterschiedlichen Burstenergien mit verschiedenen SBS-Medien haben ihre Ursache in unterschiedlichen Resonatorkonfigurationen (siehe Kap. 3.1.2.).
Für Xenon war der Effekt des Aussetzens der SBS bei einem
Resonatorlängenverhältnis von 1:2 trotz Suche aufgrund
der schwachen Fokussierung im Teleskop und der daraus folgenden
großen Wechselwirkungslänge (siehe Kap.3.1.2.) nicht
zu beobachten.
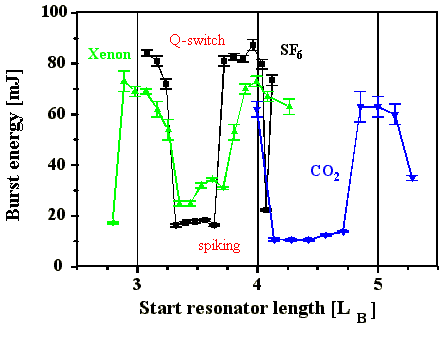
Abb. 4.2.2: Burstenergien und Pulsstabilitäten des Lasers (SF6 , CO2 und Xenon) in
Abhängigkeit von der Startresonatorlänge in Einheiten
der Brillouin-Länge
4.2.2. Transientes Modenverhalten mit SF6 als SBS-Medium
Die Auswertung der Ringstrukturen der Bilder des Fabry-Perot-Interferometers zeigen, daß bei Startresonatorlängen größer 3LB aus den äußeren Ringen kleinere Frequenzabstände zu entnehmen sind als der Brillouin-Shift, bei inneren Ringabständen darauf zulaufend (Abb. 4.2.3). Für Startresonatorlängen kleiner 3LB weisen die äußeren Ringe größere Frequenzabstände auf als der Brillouin-Shift, bei inneren Ringabständen wiederum darauf zulaufend. Die äußeren Frequenzabstände haben Werte, die dem dreifachen der jeweiligen Startresonatormodenabstände entsprechen. Bei guter Längenanpassung des Startresonators an LB beobachtet man nach Auswertung der inneren und äußeren Ringe Frequenzabstände, die dem extern gemessenen Brillouin-Shift entsprechen. Die Ringabstände in Abbildung 4.2.3 sind von außen nach innen durchnumeriert, entsprechend dem zeitlichen Verhalten. Aufgrund der fehlenden Mittelung sind die Werte stärker gestreut.
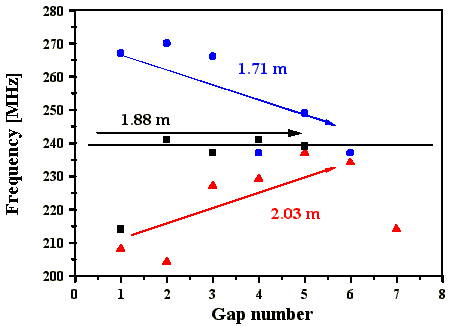
Abb. 4.2.3: Aus den FPI-Bildern ermittelte Frequenzabstände mit SF6 als SBS-Medium
für verschiedene Startresonatorlängen
Diese Zeitabhängigkeit des Brillouin-Shifts deutet
darauf hin, daß der SBS durch die longitudinalen Startresonatormoden
eine erzwungene Schwingung auferlegt wird. Diese beeinflußt
die Schallwelle innerhalb der Linienbreite der SBS derart, daß
das stimuliert gestreute Licht eine Frequenzverschiebung erfährt,
die dem Vielfachen des Startresonatormodenabstands entspricht.
Nach dem Abschalten des Startresonators relaxiert der Shift
aufgrund der Dämpfung (Phononenlebensdauer) auf seine
Mittenfrequenz nB zu.
4.2.3. Auswirkungen auf die Zeitstruktur der Pulse
Die Änderung der Startresonatorlänge hat keine Auswirkungen auf die Q-switch Pulsstruktur. Die Fouriertransformierten der Pulse zeigen ausschließlich Frequenzabstände c/2LSBS , unabhängig von der Startresonatorlänge (Abb. 4.2.4 und Abb. 4.2.6).
In Abb. 4.2.5 sind die ermittelten Pulslängen in Abhängigkeit von der Startresonatorlänge dargestellt.
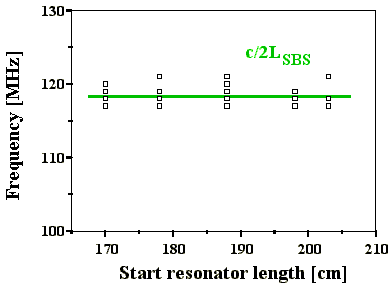
Abb. 4.2.4: Aus den Fouriertransformierten ermittelte Frequenzabstände in Abhängigkeit
von der Startresonatorlänge mit SF6 als SBS-Medium
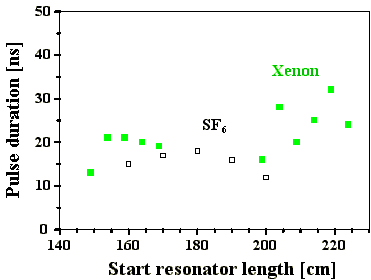
Abb. 4.2.5: Q-switch Pulslängen in Abhängigkeit von der Startresonatorlänge
mit SF6 und Xenon als SBS-Medien
Abb. 4.2.6 zeigt einen gemessenen Intensitätsverlauf und
die Fouriertransformierte für eine SBS-Resonatorlänge
von 2LB und eine Startresonatorlänge von 3LB+10 cm
mit Xenon als SBS-Medium. Abb. 4.2.7 zeigt zum Vergleich den aus
den SBS-Resonatorfrequenzen errechneten Intensitätsverlauf
und die Fouriertransformierte.
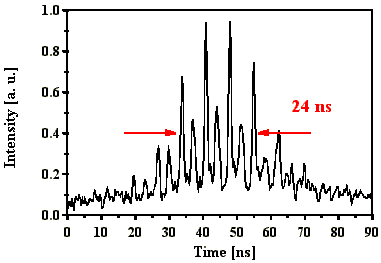
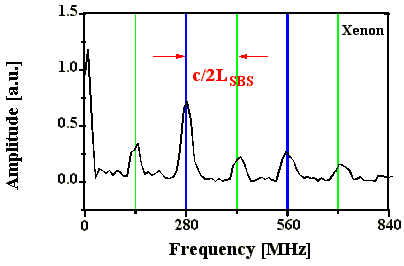
Abb. 4.2.6: Q-switch Puls und Fouriertransformierte bei einer Startresonatorlänge von
2,24 m mit Xenon als SBS-Medium
(blaue Linien entsprechen Frequenzabständen nB
)
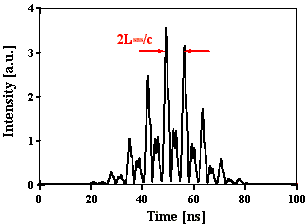
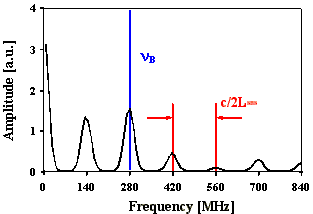
Abb. 4.2.7: Berechnete Q-switch Pulsstruktur und Fouriertransformierte für eine SBS-
Resonatorlänge von 2LB , statistischer Phase und Xenon als SBS-Medium
unter zeitlicher Berücksichtigung des Shifts
Die Ergebnisse bestätigen die Annahme, daß die Ursachen
der Q-switch Pulsstruktur im SBS-Resonator liegen. Wenn der
SBS-Resonator longitudinale Startresonatormoden übernehmen
würde, dann müßten sich die Frequenzabstände
c/2Lstart in den Fouriertransformierten der Intensitätsverläufe
der Pulse, zumindest aber eine Abhängigkeit der Pulsstruktur
von der Startresonatorlänge, nachweisen lassen.
4.3. Variation der Verluste im Startresonators mit SF6, CO2 und Xe als SBS-Medien
4.3.1. Auswirkungen auf die Pulsenergie und Pulsstabilität
Die Variation der effektiven Reflexion des Startresonatorspiegels
M2 ergibt, daß eine geringere Güte des Startresonators
zu größeren Q-switch Pulsenergien führt
[46]. Die Anzahl der Pulse im Burst nimmt bei gleicher Pumppulsdauer
mit steigenden Verlusten im Startresonator ab (Abb. 4.3.2). Daraus
folgt, daß die Burstenergie durch Variation der Verluste
im Startresonator zunimmt oder abnimmt, je nach Ausnutzung der
über die Dauer des Blitzlampenpulses aufgebauten Besetzungsinversion
(Abb. 4.3.1). Die Pulsstabilität variiert zwischen 3% und
8%. Ursache hierfür ist die Zunahme der thermischen Linsenwirkung
durch die höhere Anzahl von Graugläsern. Weiterhin zeigt
sich, daß die Pulsenergien für unterschiedliche SBS-Medien
im Rahmen der Meßgenauigkeit gleich sind. Die Burst-energien
sind aufgrund der Längenanpassung der Resonatoren an LB
und der daraus folgend unterschiedlichen Verluste des SBS-Oszillators
verschieden.
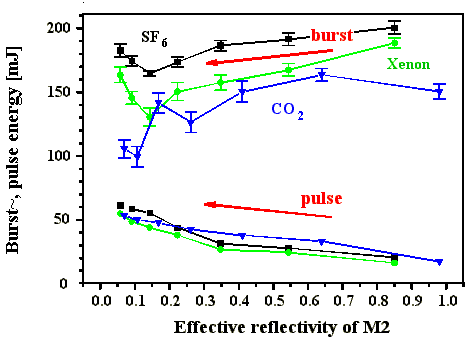
Abb. 4.3.1: Burst~ und Pulsenergien in Abhängigkeit von der Grauglastransmission im
Startresonator mit SF6 , CO2 und Xenon
als SBS-Medien
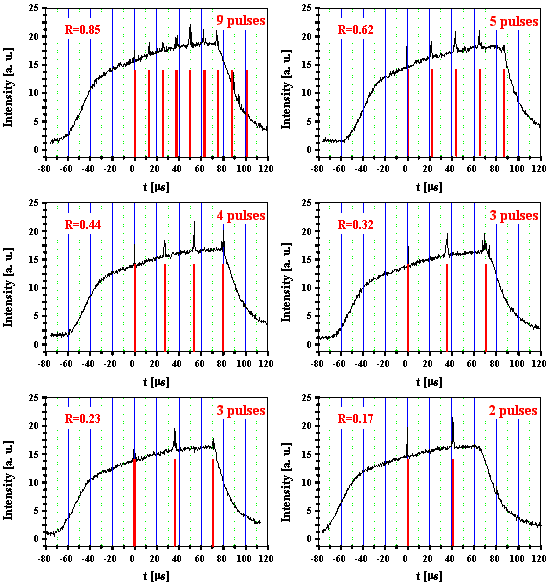
Abb. 4.3.2: Blitzlampenpulse mit Q-switch Pulsen für verschiedene Reflexionsgrade
des Startresonatorspiegels M2 mit CO2 als SBS-Medium
Aus diesen Ergebnissen folgt, daß die Pulsenergien
für SBS-Medien mit einer SBS-Schwelle im mJ-Bereich unabhängig
von der SBS-Schwelle des verwendeten Mediums sind. Entscheidend
ist neben den Verlusten im SBS-Resonator der Einsatzzeitpunkt
des ersten Spikes des Startresonators, der von den Verlusten im
Startresonator bestimmt wird. Die bis dahin aufgebaute Inversion
kann dann durch den Q-switch Puls abgebaut werden. Aufgrund des
schnellen Anstiegs der Intensität in der Spike-Flanke gegenüber
der in dieser Zeit abgebauten Inversion führt eine höhere
SBS-Schwelle weder zu einer höheren noch zu einer niedrigeren
Pulsenergie. Die Spike-Einsatzzeit korreliert sehr gut mit der
Einsatzzeit des Q-switch Pulses [47].
4.3.2. Auswirkungen auf die Zeitstruktur der Pulse
Es zeigt sich, daß mit geringerem effektiven Reflexionsgrad
des Spiegels M2 die Durchmodulation der Pulse stärker
wird. Die Peaks der Schwebungsfrequenzen der SBS-Resonatorfrequenzen
in den Fouriertransformierten sind stärker ausgeprägt
(Abb. 4.3.3 und Abb. 4.3.4) und die Pulsdauer nimmt ab
(Abb. 4.3.5). Der Übergang vom Spiking-Verhalten bei hoher
effektiver Reflektivität des Spiegels M2 zur Güteschaltung
bei geringer Reflektivität ist nicht abrupt. Mit abnehmender
Reflektivität verkürzen sich die Spike-Pulse allmählich,
ihr zeitlicher Abstand erhöht sich. Von einer Güteschaltung
kann erst gesprochen werden, wenn die Pulse über die gesamte
Pumppulsdauer mit zeitlich gleichem Abstand und nahezu gleicher
Energie auftreten (Burst).
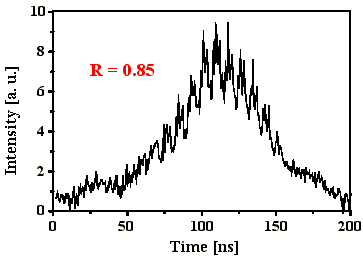
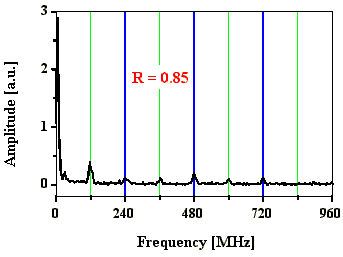
Abb. 4.3.3: Q-switch Puls und Fouriertransformierte bei einem effektiven Reflexionsgrad
von 0,85 mit SF6 als SBS-Medium
(blaue Linien entsprechen Frequenzabständen nB
)
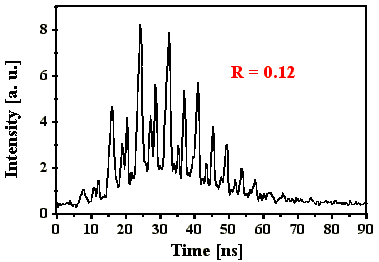
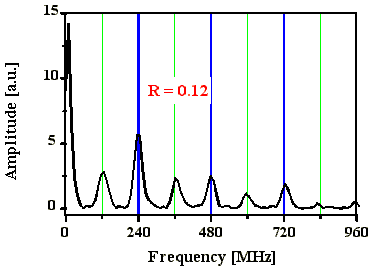
Abb. 4.3.4: Q-switch Puls und Fouriertransformierte bei einem effektiven Reflexionsgrad
von 0,12 mit SF6 als SBS-Medium
(blaue Linien entsprechen Frequenzabständen nB
)
Bei einem effektiven Reflexionsgrad des Startresonatorspiegels
M2 von 1 tritt keine Güteschaltung auf, es ist typisches
Spiking mit Spike-Pulslängen von ca. 400 ns und Pulsabständen
von ca. 5-10 ms zu beobachten.
Die Fouriertransformierte dieser Intensitätsverläufe
läßt nur Startresonatormodenabstände erkennen.
Durch leichte Erhöhung der Verluste im Startresonator, z.B.
durch Verstimmen der Teleskoplänge, ist es möglich,
die Startresonatormoden so zu beeinflussen, daß nur Startresonatormoden
mit Frequenzabstand von nB
oszillieren. Trotzdem zeigt der Resonator typisches Spiking.
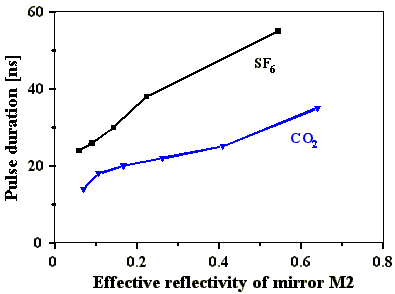
Abb. 4.3.5: Q-switch Pulslänge in Abhängigkeit vom effektiven Reflexionsgrad des
Spiegels M2 mit SF6 und CO2 als SBS-Medien
4.4 Variation der Fokussierung in der SBS-Zelle mit SF6 als SBS-Medium
4.4.1. Auswirkungen auf die Pulsenergie und Pulsstabilität
Die Pulsstabilität der Q-switch Pulse des Oszillators ändert sich für unterschiedliche Fokussierung im Teleskop nicht (Abb. 4.4.1). Die unterschiedlichen Pulsenergien ergeben sich aus unterschiedlichen effektiven Reflexionsgraden des Startresonatorspiegels M2. Diese waren notwendig, da sich zur eindeutigen Zuordnung der FPI-Bilder zu den Pulsstrukturen nur ein Q-switch Puls während einer Blitzlampenpulsdauer bilden durfte.
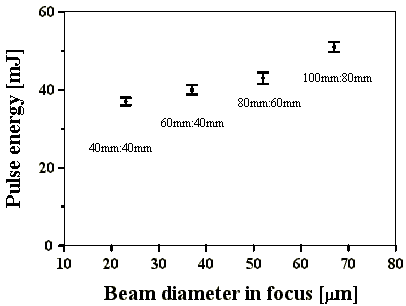
Abb. 4.4.1: Q-switch Pulsenergien und Pulsstabilitäten in Abhängigkeit vom
berechneten Strahldurchmesser im Teleskopfokus mit SF6 als SBS-Medium
und verschiedene Verluste im Startresonator
Diese Ergebnisse lassen darauf schließen, daß die
Kohärenzlänge des Lichts des Startresonators um ein
Vielfaches größer ist als die Wechselwirkungslänge
im SBS-Medium. Die Fokussierung zu kleineren Strahlradien wird
durch die optische Durchbruchsfestigkeit des SBS-Mediums begrenzt,
die zu größeren Strahlradien durch die für die
SBS notwendige Kohärenzlänge des Startresonatorlichts.
Diese ist abhängig von der spektralen Breite des Verstärkungsprofils
des aktiven Mediums (Nd:YALO-30 GHz), von der Startresonatorlänge
und von den Verlusten im Startresonator. Desweiteren wird die
Fokussierung dadurch bestimmt, daß die gewünschte Phasenkonjugation
nur unter der Bedingung kleiner Wechselwirkungslänge auftritt
[7].
4.4.2. Auswirkungen auf die Zeitstruktur der Pulse
In Abb. 4.4.2 sind die Pulslängen der Q-switch Pulse über den berechneten Strahldurchmessern im Fokus der realisierten Teleskope aufgetragen. Es ist eine Veränderung der Einhüllenden der Pulsmodulationen zu beobachten. Mit steigendem Strahldurchmesser im Fokus flacht die abfallende Flanke des Pulses immer mehr ab (Abb. 4.4.3).
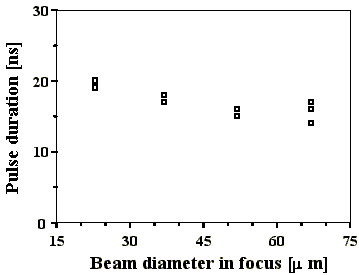
Abb. 4.4.2: Q-switch Pulslängen in Abhängigkeit vom berechneten Strahldurchmesser
im Fokus des Teleskops mit SF6 als SBS-Medium und
verschiedene RM2
Die Fouriertransformierten der Intensitätsverläufe zeigen
Frequenzabstände mit c/2LSBS , die aus den FPI-Bildern
ermittelten Frequenzabstände entsprechen dem Brillouin-Shift,
unabhängig von der Fokussierung im Teleskop.
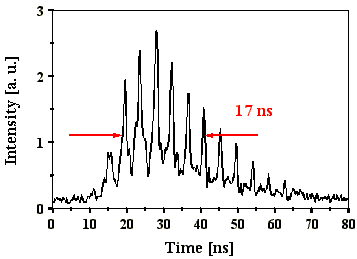
Abb. 4.4.3: Q-switch Puls des Resonators mit 100 mm:80 mm Teleskop
mit SF6 als SBS-Medium
4.5. Untersuchungen zur Phasenkonjugation mit SF6 als SBS-Medium
4.5.1. Energiereflexion in Abhängigkeit von den Verlusten im Startresonator
Die Messung des Energiereflexionsgrads der SBS ohne
Aberrator im SBS-Resonator zeigt, daß er für die
gewählte Fokussierung im Teleskop einen Wert von 65%
nicht übersteigt. Die durch die Zelle verursachten Verluste
liegen zwischen 12% und 16% (Abb. 4.5.1). Das Optimum
der SBS-Reflektivität liegt bei einem effektiven Reflexionsgrad
des Startresonatorspiegels M2 von 0,10 bis 0,30. Unter
0,10 sinkt sie ab, über 0,40 ist die SBS-Reflexion zu gering,
so daß zu viel Energie durch die Zelle verloren geht.
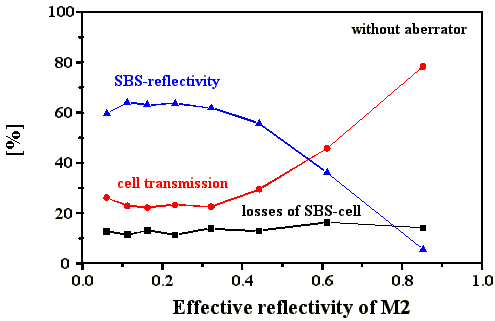
Abb. 4.5.1: SBS-Reflektivität, Transmission und Verluste der Zelle in Abhängigkeit von
der effektiven Reflektivität des Startresonatorspiegels
M2 (ohne Aberrator)
Die allmähliche Zunahme der SBS-Reflektivität bei Verringerung des effektiven Reflexionsgrads des Spiegels M2 erklärt die in Kap. 4.3. erläuterten Beobachtungen. Die Tatsache, daß die Energiereflektivität einen Wert von 65% nicht überschreitet, könnte damit erklärt werden, daß die Leistungsreflexion der SBS zeitabhängig ist und daß aufgrund der recht hohen SBS-Schwelle des SF6 in der Flanke des Spike-Pulses des Startresonators zu viel Energie transmittiert wird (siehe Kap. 4.1.3). Der Reflexionsgrad der SBS nimmt bei zu geringer Güte des Startresonators wieder ab, da das von M2 reflektierte Licht zu geringe Intensität hat und deshalb nicht mehr so effektiv zur Schwellabsenkung der SBS beitragen kann.
Bei den Messungen mit Aberrator im SBS-Resonator übersteigen
die Energiereflexionswerte nicht 60%. Die durch
die Zelle verursachten Verluste liegen zwischen 17% und 20% (Abb. 4.5.2).
Das Optimum der SBS-Reflektivität liegt wieder bei
einem effektiven Reflexionsgrad des Startresonatorspiegels von
0,10 bis 0,30.
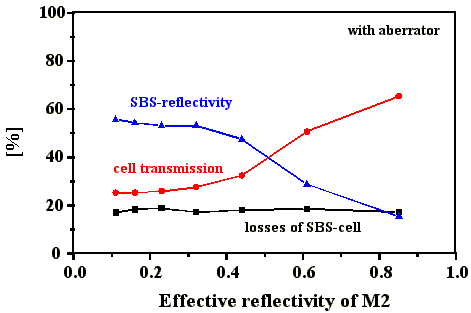
Abb. 4.5.2: SBS-Reflektivität, Transmission und Verluste der Zelle in Abhängigkeit von
der effektiven Reflektivität des Startresonatorspiegels
M2 (mit Aberrator)
Der Vergleich der Energiereflexionsgrade der SBS ergibt, daß stärkere Aberrationen im Resonator zu einer geringeren Reflektivität führen. Ursache hierfür könnte die Aufweitung der Strahlquerschnittsfläche im Fokus des Teleskops durch die Phasenstörungen sein. Die Intensität in den Flanken des aberrierten Gaußstrahls erreicht nicht mehr die SBS-Schwelle, das nicht reflektierte Licht wird transmittiert oder spontan gestreut. Daraus ergäben sich auch die gegenüber dem Resonator ohne Aberrator erhöhten Verluste der Zelle sowie die höhere Transmission der SBS-Zelle. Die durch die Zelle verursachten Verluste entstehen durch insgesamt 8 optische, entspiegelte Oberflächen der Teleskoplinsen und Zellenfenster mit einer Gesamtreflektivität von ca. 8% pro Durchgang und durch zusätzliche Beugungs- und Streuverluste. Für den Resonator ohne Aberrator ergeben sich neben den Reflexionsverlusten der Oberflächen Beugungs- und Streuverluste von ca. 5% und für den Resonator mit Aberrator von ca. 10%.
Die Burstenergien des Resonators mit Aberrator sind kleiner als
beim Resonator ohne Aberrator, die Pulsenergien sind vergleichbar.
Das ist auf Reflexionsverluste und Streuverluste im Resonator
durch den Aberrator von 25%5% pro Umlauf zurückzuführen
(Abb. 4.5.3). Zur Verlustberechnung des Aberrators wurde
die einfallende Energie mit der zweimal durch den Aberrator transmittierten
Energie (HR-Spiegel hinter Aberrator) ins Verhältnis gesetzt.
Daraus ergibt sich ein zusätzlicher Verlust von ca. 25%
pro Umlauf und ca. 13% pro Durchgang. Dieser Wert wurde zur
Berechnung der Energiereflexionsgrade des Resonators mit Aberrator
verwendet.
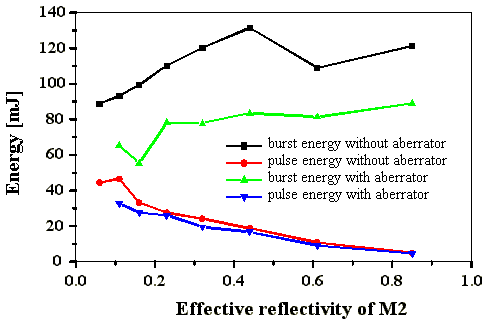
Abb. 4.5.3: Vergleich der Burst- und Pulsenergien mit und ohne Aberrator
im SBS-Resonator
In Abb. 4.5.3 ist wieder das typische Verhalten der Burstenergien
zu erkennen. Je nach Ausnutzung der über den Blitzlampenpuls
aufgebauten Besetzungsinversion sinkt und steigt die Burstenergie,
die Pulsenergien wachsen an. Die Verluste im SBS-Resonator durch
den Aberrator von 25% pro Umlauf haben im Rahmen der Meßgenauigkeit
keine Auswirkungen auf die Pulsenergien. Dies könnte damit
erklärt werden, daß diese Verluste die Laserschwelle
des Startresonators erhöhen, was zu einem späteren Einsatzzeitpunkt
des Spikings und damit zu einer höheren Inversion führt.
Diese höhere Inversion kann aber nach der Güteschaltung
nicht zu einer höheren Pulsenergie und kürzeren Pulsdauer
führen, da diese Verluste auch im SBS-Resonator wirken. Die
Verluste durch den Aberrator bewirken eine kleinere Pulsanzahl,
was zu der geringeren Burstenergie führt.
4.5.2. Verluste am Pinhole mit und ohne Aberrator im SBS-Resonator
Die Energieverluste am Pinhole lagen für den Resonator ohne
Aberrator zwischen 5% und 10%, für den Resonator mit Aberrator
zwischen 1% und 5%. Eine Abhängigkeit von der Startresonatorgüte
war nicht zu erkennen (Abb. 4.5.4).
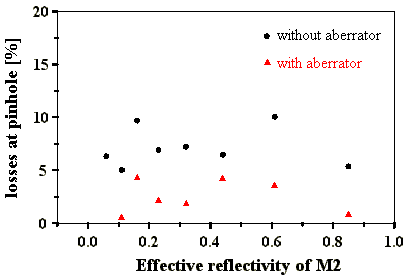
Abb. 4.5.4: Vergleich der Verluste am Pinhole mit und ohne Aberrator in Abhängigkeit
von der effektiven Reflexion des Startresonatorspiegels M2
Die geringeren Energieverluste am Pinhole für den Resonator mit Aberrator sind ein Indiz für die Phasenkonjugation durch die SBS im Resonator. Da die SBS aber auch als Raumfilter wirkt, indem sie die am Ort des Fokus außen liegenden höheren Ortsfrequenzen mit geringer Intensität nicht reflektiert, verbessert sie auch so die Strahlqualität [48]. Dies würde sich in einer erhöhten Transmission bemerkbar machen, welche auch zu beobachten ist (Kap. 4.5.1). Dieser Effekt könnte die geringeren Verluste am Pinhole erklären. Er ist aber unerwünscht, da dadurch die Effizienz des SBS-Oszillators sinkt.
Die Auswertung der zeitlichen Pulsstrukturen des am Pinhole gestreuten Lichts und des transmittierten Lichtes ergibt, daß die Verluste am Pinhole zum Pulsende hin abnehmen (Abb. 4.5.5 und Abb. 4.5.6). Diese Zeitabhängigkeit der Verluste am Pinhole ist wiederum ein Indiz für die Phasenkonjugation durch die SBS im Resonator. Da der Vergleich zu einem Q-switch Puls ohne Einsatz der SBS aber fehlt, ist es auch möglich, daß die Ausbildung der transversalen Modenstruktur zu dieser Zeitabhängigkeit der Verluste am Pinhole führt.
Für die Zeitabhängigkeit der Verluste am Pinhole aufgrund
der Phasenkonjugation der SBS könnte sprechen, daß
der transversale Mode schon durch den Startresonator gebildet
und das vorhandene Strahlungsfeld in diesen Experimenten vom SBS-Resonator
übernommen wurde. Die Verluste am Pinhole zeigen für
den Resonator mit Aberrator aber keine starke Zeitabhängigkeit.
Dieser Effekt könnte wieder durch die Wirkung der SBS als
Raumfilter erklärt werden. Die Strahlqualität wäre
besser mit daraus folgenden geringeren und zeitlich konstanten
Verlusten am Pinhole. Die Modulation der Verlustkurve resultiert
aus der Mittelung der aufgenommenen Intensitätsverläufe
über unterschiedliche Pulse.
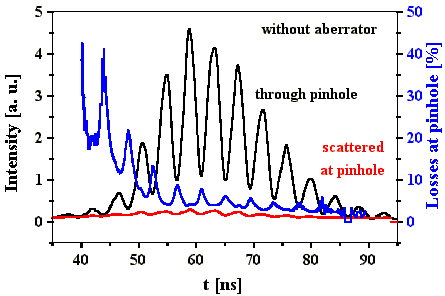
Abb. 4.5.5: Zeitliche Abhängigkeit der Verluste
(blau) am Pinhole (ohne Aberrator)
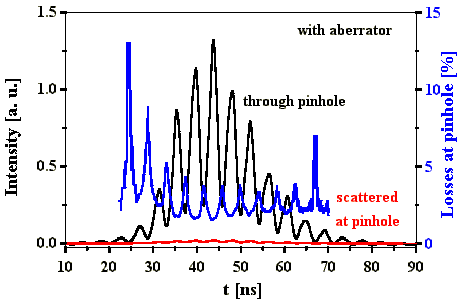
Abb. 4.5.6: Zeitliche Abhängigkeit der Verluste
(blau) am Pinhole (mit Aberrator)
4.5.3. Leistungsreflexion der SBS
Die Abb. 4.5.7 zeigt die zeitliche Pulsstruktur eines in die SBS-Zelle einfallenden (schwarz) und des reflektierten Pulses (grün) für einen effektiven Reflexionsgrad des Startresonatorspiegels M2 von 0,12 ohne Aberrator im SBS-Resonator.
Die dargestellten Pulsstrukturen sind über 10 Pulse gemittelt. Die Intensitäten der einfallenden und reflektierten Pulse sind über die Energiereflexion normiert (Kap. 3.2.). Die durch Quotientenbildung aus einfallender und reflektierter Intensität gewonnene Leistungsre-flexionskurve (blau) läßt erkennen, daß der Leistungsreflexionsgrad vergleichbar mit dem Energiereflexionsgrad ist, da er auch Werte um 65% erreicht. Am Pulsanfang steigt die Leistungsreflexionskurve an, sie geht dann in ein Plateau über. Die Modulation der Leistungsreflexion entsteht durch die Mittelung über unterschiedliche Pulse. Diese war notwendig, da zur Erhöhung der Genauigkeit nur eine Vakuum-Photodiode verwendet wurde.
Aus dieser Messung folgt, daß der Energiereflexionsgrad
auf den über den Puls konstanten Leistungsreflexionsgrad
zurückzuführen ist. Die am Pulsanfang und Pulsende transmittierte
Energie hat vernachlässigbaren Einfluß auf den Energiereflexionsgrad
der SBS.
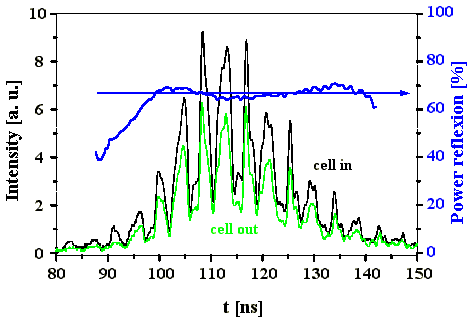
Abb. 4.5.7: Intensitätsverlauf (energienormiert, gemittelt über 10 Pulse) eines Pulses
und Leistungsreflexionsgrad der SBS (gemittelt über 10 ns)
bei einem effektiven Reflexionsgrad von M2 von 0,12
4.5.4. Abschätzung zur Schwellabsenkung der SBS im Resonator
Zur Abschätzung der SBS-Schwelle im Resonator wurde die in
Kap. 4.5.1 ermittelte SBS-Reflektivität (Energiereflexionsgrad)
für den Resonator ohne Aberrator über der in die Zelle
einfallenden Pulsenergie aufgetragen (Abb. 4.5.9). Diese ist wiederum
abhängig von der Startresonatorgüte. Daraus ergibt sich,
daß die extern gemessene SBS-Schwelle (10,5 mJ,
30 ns FWHM, longitudinaler Monomode) um einen Faktor
von etwa 4-6 erniedrigt wird. Dabei ist aber zu berücksichtigen,
daß im Resonator kein longitudinaler Monomode vorliegt und
daß sich die Pulslängen mit der Startresonatorgüte
ändern. Im Resonator wird die maxi-male SBS-Reflektivität
bei kleineren Pulsenergien erreicht als extern. Ein Grund für
den geringen maximalen Reflexionsgrad könnte die Frequenzstruktur
des SBS-Resonators sein. Die Schwebungen dieser Frequenzen führen
zu einer zeitlich stark schwankenden Intensität am Ort der
Reflexion und damit möglicherweise zu einer schlechteren
Leistungsreflexion.
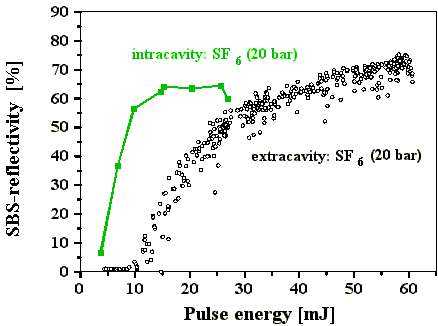
Abb. 4.5.9: SBS-Reflektivitäten in Abhängigkeit von der einfallenden Pulsenergie
(extern und intern) mit SF6 als SBS-Medium
5. Zusammenfassung und Diskussion der Ergebnisse
5.1. Longitudinale Modenstruktur
Die in Kap. 4.1. bis 4.4 dargestellten Ergebnisse können
wie folgt zusammengefaßt werden.
Die Bilder des Fabry-Perot-Interferometers lassen Frequenzabstände
erkennen, die sehr gut mit den extern gemessenen Brillouin-Shifts
der jeweiligen Medien übereinstimmen. Die Frequenzabstände
korrelieren nicht mit der SBS-Resonatorlänge und nur in einem
von 10 Fällen mit der Startresonatorlänge (zeitweilige
Beobachtung von einem Startresonatormodenabstand). Daraus läßt
sich schließen, daß diese Frequenzabstände den
Brillouin-Shift repräsentieren.
Die Fouriertransformierten der zeitlichen Intensitätsverläufe
der Q-switch Pulse zeigen ausschließlich Frequenzabstände,
die den Modenabständen eines Fabrry-Perot-Resonators der
gewählten SBS-Resonatorlänge entsprechen. Frequenzabstände
entsprechend dem Brillouin-Shift sind nur zu erkennen, wenn sie
Vielfachen der SBS-Resonatormodenabstände entsprechen.
Die FPI-Bilder leicht längenverstimmter Startresonatoren
zeigen Frequenzabstände, die Vielfachen der Startresonatormodenabstände
entsprechen. Diese relaxieren während des Pulses auf die
Mittenfrequenz der Linienbreite der SBS zu.
Die Längenanpassung des SBS-Resonators an den Brillouin-Shift
ist zur Gewährleistung der Stabilität der Pulsenergien
entgegen bisherigen Annahmen [15, 46, 49, 50] nicht
notwendig. Die Längenanpassung des Startresonators an die
Brillouin-Länge ist für die Schwellabsenkung der SBS
unbedingt notwendig. Die Anpassung beider Resonatoren an LB
führt zu regelmäßig modulierten Pulsen.
Bei einem Verhältnis von Startresonatorlänge zu SBS-Resonatorlänge
von 2:1 setzte die SBS aus. Der Startresonator oszillierte mit
geringer Güte. Es wurde kein anderes Resonatorlängenverhältnis
beobachtet, bei dem dieser Effekt auftrat.
Die Q-switch Pulsenergien waren entgegen bisherigen Annahmen [15, 46, 47]
unabhängig von der SBS-Schwelle der verwendeten Materialien.
Die Q-switch Pulse wachsen aus den Spike-Flanken des Startresonators
heraus. Die Q-switch Pulsenergien skalieren mit den Verlusten
im Startresonator. Die Modulationstiefe der Pulse erhöht
sich mit geringerer Startresonatorgüte und die Pulse werden
kürzer.
Aus den Ergebnissen resultieren folgende Hypothesen:
Die in den FPI-Bildern erkennbaren Frequenzabstände nB
sind in den Fouriertransformierten der Intensitätsverläufe
nicht zu erkennen. Sie können von der PIN-Diode nicht als
Schwebung in der Intensität detektiert werden, da sie zeitlich
nacheinander auftreten. Aus der Tatsache, daß die Frequenzabstände
des Laserlichts des SBS-Resonators nicht in den FPI-Bildern zu
erkennen sind, aber in den Fouriertransformierten der Intensitätsverläufe
der Pulse, folgt, daß die Intensität der SBS-Resonatorfrequenzen
gegenüber der der sichtbaren Grundfrequenz gering ist (siehe
Kap. 2.5). Die Bildung der Lichtwellen mit spektralem Abstand
c/2LSBS im SBS-Resonator ist wahrscheinlich nur eine
Randerscheinung des Schaltprozesses der SBS.
In den Fouriertransformierten der Intensitätsverläufe
der Pulse ist auch im Resonanzfall selten mehr als eine Schwebungsfrequenz
mit spektralem Abstand nB
stark ausgeprägt (1). Bei einem Resonatorlängenverhältnis
von 1:2 (LSBS : Lstart) setzt die SBS aus
(2). Andere Resonatorlängenverhältnisse, bei denen die
SBS aussetzt, wurden nicht beobachtet. Das legt den Schluß
nahe, daß für den Schaltprozeß der SBS nur zwei
(1) durch spontane Brillouin-Streuung gekoppelte longitudinale
Moden des Startresonators mit einem spektralen Abstand von nB
und einer Phasendifferenz von 2p (2)
verantwortlich sein könnten.
Die Startresonatormoden des verstimmten Resonators regen die SBS
zu einer erzwungenen Schwingung an und erzwingen damit einen vom
extern gemessenen Wert abweichenden Brillouin-Shift (siehe Kap.
4.2.2.). Nach dem Abschalten des Startresonators relaxiert das
System auf seine Mittenfrequenz zu. Die Dauer dieser Relaxation
wird wahrscheinlich durch die Lebensdauer der Schallwelle bestimmt.
Weiterführende Literatur zur longitudinalen Modenstruktur
von SBS-Oszillatoren ist in [51, 52, 53] zu finden.
Die im Rahmen dieser Diplomarbeit gewonnenen Erkenntnisse führen zu folgender Hypothese des Schaltprozesses der SBS.
Nach Erreichen der Laserschwelle im Startresonator wächst
die Intensität des Lichts im ersten Spike stark an. Zwei
longitudinale Moden des an LB angepaßten Startresonators
mit spektralem Abstand des Brillouin-Shifts nB
und hoher Intensität koppeln aufgrund der spontanen Brillouin-Streuung
mit einer Phasendifferenz von 2p. Sie
sind auf den Startresonatorspiegeln in Phase, in der Mitte des
Resonators ist die Phasenverschiebung gleich p.
Das führt dazu, daß dort die Einhüllende der Schwebung
ein Minimum hat und somit auch die Intensität. Berechnungen
hierzu wurden von Schumann in [15] gemacht. Beide Startresonatormoden
oszillieren mit nahezu gleicher Intensität. Die vom Startresonatorspiegel
M2 reflektierten Moden mit entsprechend geringerer Intensität
(Abb. 5.1) interferieren mit den einfallenden.
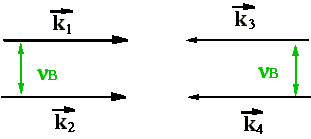
Abb. 5.1: Longitudinale Startresonatormoden mit spektralem Abstand nB
k1, k2
vom Auskoppler, k3,
k4 vom Startresonatorspiegel
Die entstehenden Schwebungen könnten via Elektrostriktion Ursache einer stehenden Dichtemodulation im Medium sein, da das SBS-Medium ein schwingungsfähiges System darstellt. Der Abstand der Maxima der Dichtemodulation (Schallwellenlänge) wäre vom Modenabstand des Startresonators abhängig. Diese stehende Dichtemodulation könnte über das Superpositionsprinzip auch als zwei entgegengesetzt laufende Schallwellen aufgefaßt werden.
Zwischen dem stehenden Schallwellengitter und dem Auskoppelspiegel
könnten sich longitudinale SBS-Resonatormoden ausbilden.
Dieser Effekt könnte durch elastische Streuprozesse oder
durch 1) Stokes- und 2) Anti-Stokes-Streuung erklärt werden
(Abb. 5.2). Dabei könnte das Licht beim ersten Umlauf unter
Richtungsumkehr Stokes gestreut und beim zweiten Umlauf unter
Richtungsumkehr Anti-Stokes gestreut werden.
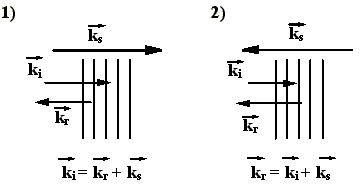
Abb. 5.2 Teilprozesse: 1) Stokes-Streuung 2)
Anti-Stokes-Streuung
Die Impulse der einlaufenden Lichtwellen ki könnten von den Schallwellen aufgenommen bzw. abgegeben werden (Abb. 5.2 ), so daß das zweimal reflektierte Licht nicht frequenzverschoben ist. Das nach zwei Umläufen verstärkte und nicht frequenzverschobene Licht schwächt bei jeder Reflexion die Anti-Stokes-Welle, stärkt die Stokes-Welle und erhöht die Reflektivität der SBS. Der Startresonator würde abschalten, die Anti-Stokes-Welle zusammenbrechen.
Im verstimmten Fall würde nur eine der beiden Startresonatormoden vom SBS-Resonator übernommen, die zweite würde absterben, da ihr Modenabstand nicht der SBS-Resonatorlänge angepaßt ist. Dies würde erklären, daß beim verstimmten SBS-Resonator in den Fouriertransformierten der Intensitätsverläufe der Pulse keine Frequenzabstände des Brillouin-Shifts zu erkennen sind. Nur im sehr gut abgestimmten Fall könnten beide Startresonatormoden mit Frequenzabstand nB vom SBS-Resonator übernommen werden. Das könnte Pulsstrukturen erklären, die keine Frequenzabstände der SBS-Resonatorfrequenzen aufweisen sondern nur zwei ausgeprägte Frequenzen mit Abstand nB.
Im Falle eines leicht längenverstimmten Startresonators würde dem System durch die Startresonatormoden eine erzwungene Schwingung auferlegt. Nach dem Abschalten des Startresonators könnte die Frequenzverschiebung des in der SBS-Zelle reflektierten Lichtes auf das Maximum der Resonanzstelle relaxieren.
Vereinzelt könnten auch 2 Startresonatormoden im SBS-Resonator
mit entsprechendem Modenabstand vom SBS-Resonator übernommen
werden. Beide Frequenzen könnten mit einem zeitlich so großem
Abstand existieren, daß sie in den FPI-Bildern, ihre Schwebungsfrequenz
aber nicht in der Fouriertransformierten der Intensitätsverläufe
der Pulse zu erkennen wären.
5.2. Qualität der Phasenkonjugation
Die Untersuchungen haben ergeben, daß das SBS-Medium nach
den Kriterien geringer Absorption, hoher optischer Durchbruchsfestigkeit,
eines relativ hohen Brillouin-Shifts und kurzer Schallwellenlebensdauer
gewählt werden sollte. Ein hoher Brillouin-Shift ermöglicht
aufgrund der daraus folgenden kurzen Brillouin-Länge eine
Vielzahl von Anpassungsmöglichkeiten der Startresonatorlänge
und den Aufbau kurzer Resonatoren. Eine geringe Schallwellenlebensdauer
ermöglicht eine höhere Unabhängigkeit der Schallwelle
von der durch der Startresonator erzeugten Startschallwelle. Diese
beinhaltet die falschen Phaseninformationen, so daß bei
zu langer Lebensdauer der Schallwelle die durch die optischen
Elemente des SBS-Resonators verursachten Phasenstörungen
nicht vollständig kompensiert werden können. Die Verwendung
von SBS-Medien mit geringer Schwelle und kurzer Schallwellenlebensdauer
könnte die Qualität der Phasenkonjugation entscheidend
verbessern.
Zur Optimierung dieses SBS-Oszillators wurden folgende Ergebnisse
herangezogen:
- Die Startresonatorlänge muß zur Schwellherabsetzung der SBS
an die Brillouin-Länge angepaßt werden.
- Die Anpassung des SBS-Resonators an LB ist nicht notwendig.
- Die starke thermische Linse des Nd:YALO Stabes kann zur alleinigen
Fokussierung des Lichts in die Zelle genutzt werden.
- Die Nutzung von CO2 als SBS-Medium bietet aufgrund des hohen Brillouin-
Shifts eine Vielzahl von Anpassungsmöglichkeiten des Startresonators an LB.
- Die Nutzung eines Pinholes im SBS-Resonator als Modenblende,
Raumfilter und Zerstörschutz ist von Vorteil.
Die Vorzüge dieses optimierten SBS-Oszillators liegen in
seiner Kompaktheit und Unanfälligkeit gegen Dejustage. Da
er keine weiteren Linsen enthält, ist er auch wesentlich
leichter zu justieren. Der Nachteil der starken thermischen Linse
des Nd:YALO wird bei diesem Konzept genutzt. Je stärker die
thermische Linse, um so kürzer kann der Oszillator konzipiert
werden. Der Astigmatismus der thermischen Linse des Nd:YALO stellt
für hohe Pumpleistungen ein Problem dar, da sich die Stabilitätsbereiche
des Startresonators für die Komponenten der Brechkräfte
trennen. Diese Trennung muß durch eine Astigmatismuskompensation
rückgängig gemacht werden. Ein Nachteil des kompakten
Resonators besteht darin, daß er nur bei einer Pumpleistung
betrieben werden kann, für die er berechnet und konzipiert
wurde.
6.1. Messung der thermischen Linse
Zur Berechnung des Resonators war es notwendig, die Abhängigkeit der thermischen Linse des aktiven Mediums von der mittleren Pumpleistung zu kennen. Dazu wurde ein asymmetrischer Plan-Plan-Resonator mit einer optischen Länge von 1,04 m und einem Abstand von Stabendfläche zu Auskoppelspiegel von 64 cm aufgebaut. Der Strahlverlauf im Resonator hängt von der thermischen Linse des Nd:YALO ab. Mit wachsender Pumpleistung erhöht sich die Linsenwirkung des Stabes, der Strahldurchmesser auf dem Auskoppler zieht sich zusammen. Daraus resultiert eine Abnahme der Ausgangsenergie an der Stabilitätsgrenze. Die Stabilitätsgrenze läßt sich damit aus der Darstellung der mittleren Ausgangsleistung über der mittleren Pumpleistung ermitteln.
Nd:YALO ist ein doppelbrechender Kristall. Er weist zwei Komponenten der thermische Linse auf, eine parallel zur Polarisationsrichtung des emittierten Lichtes, die andere senkrecht dazu. Diese unterschiedlichen Komponenten führen bei hohen Pumpleistungen zu einem astigmatischem Strahlverlauf im Resonator. Dieser wirkt sich negativ auf die Stabilität des Startresonators aus.
Die Pumpleistung wurde schrittweise erhöht und dazu jeweils
die Ausgangsenergie aufgenommen. (Abb. 6.1.1). Aus den Pumpleistungen
an den Stabilitätsgrenzen und der Resonatorgeometrie wurden
die Komponenten der Brechkräfte der thermischen Linse bestimmt
[17]. Für die Komponente senkrecht zur Polarisationsrichtung
des emittierten Lichtes ergab sich ein Wert von 3,8 dpt/kW
(blau), für die parallele Komponente ein Wert von 3,5 dpt/kW
(grün). Der Astigmatismus der thermischen Linse des verwendeten
Nd:YALO-Stabes beträgt damit ca. 10% der stärkeren Brechkraftkomponente.
Für mittlere Pumpleistungen über 2 kW ist zu Gewährleistung
der Stabilität des gewählten Startresonators eine Kompensation
des Astigmatismus der thermischen Linse unvermeidbar. Abb. 6.1.2
zeigt die berechneten Stabilitätsbereiche des Resonators
für beide Brechkräfte. Es ist zu erkennen, daß
der Überlapp beider Stabilitätsbereiche für hohe
Pumpleistungen kleiner wird. Insbesondere für Resonatoren,
die an den Stabilitätsgrenzen betrieben werden, ist die Astigmatismuskompensation
von besonderer Bedeutung.
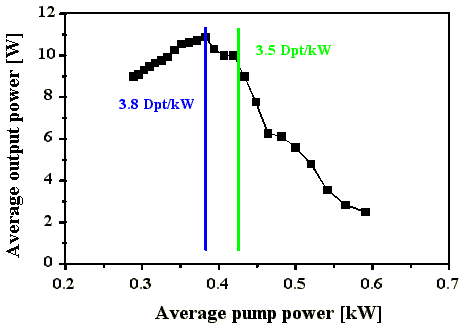
Abb. 6.1.1: Mittlere Ausgangsleistung über der mittleren Pumpleistung zur
Bestimmung der thermischen Linse und des Astigmatismus
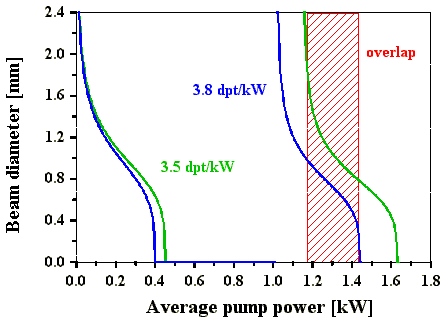
Abb. 6.1.2: Berechnete Stabilitätsbereiche für beide Brechkräfte (Strahldurchmesser
auf dem Auskoppler)
Strahlprofile auf dem Auskoppler für anwachsende Pumpleistungen, 1. und 2. Stabilitätsbereich
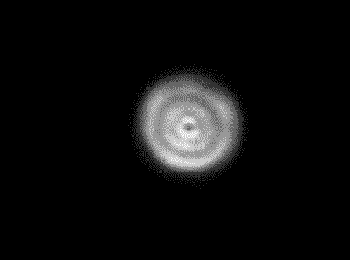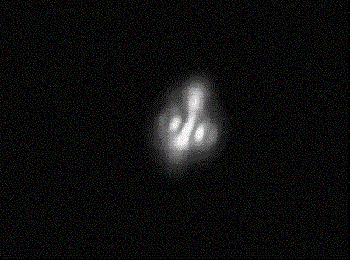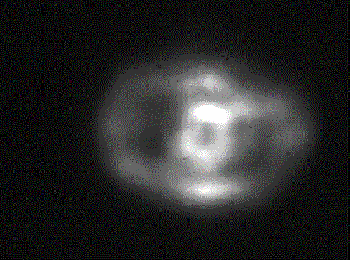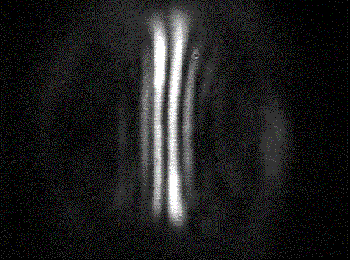
1. und 2. Stabilitätsbereich
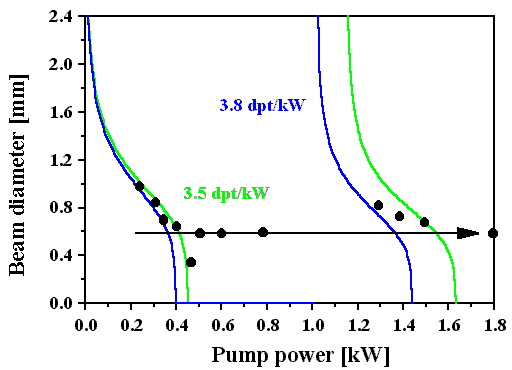
Den Startresonator bilden der Auskoppelspiegel M1 (Abb. 6.2.1)
mit einem Krümmungsradius von 200 mm und einem Reflexionsgrad
von 25%, der Nd:YALO und der Spiegel M2 mit einem Krümmungsradius
von 70 mm und einem Reflexionsgrad von 50%. Der SBS-Resonator
hatte eine geometrische Länge von 0,84 m, als SBS-Medium
wurde CO2 benutzt. Die optische Startresonatorlänge
betrug 1,02 m (geometrisch 0,93 m), das dreifache der
Brillouin-Länge LB des CO2. Ein Pinhole
mit einem Durchmesser von 442 mm
diente als Blende zur Selektion des TEM00 und als Raumfilter.
Um in der SBS-Zelle einen möglichst kleinen und am Pinhole
einen Fokusdurchmesser von ca. 300 mm
zu realisieren, wurde der Resonator asymmetrisch aufgebaut. Zur
Erzielung eines großen Modenvolumens wurde an der Grenze
des zweiten Stabilitätsbereichs gearbeitet. Abb. 6.2.2 zeigt
den berechneten Strahlverlauf im Resonator.
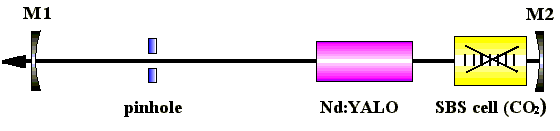
Abb. 6.2.1: Schematischer Aufbau des kompakten Resonators
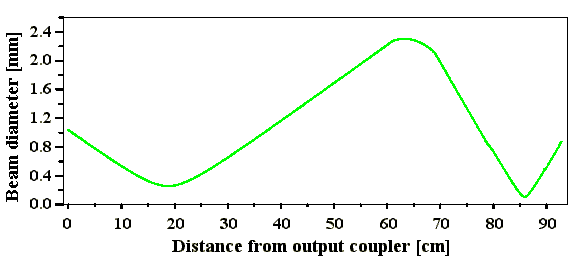
Abb. 6.2.2: Berechneter Strahlverlauf für den kompakten Resonator bei einer mittleren
Pumpleistung von 2,08 kW
Der SBS-Oszillator wurde bei einer Pumppulsenergie von 33 J, 1 ms Pulsdauer und einer Repetitionsrate von 53 Hz betrieben. Die mittlere Ausgangsleistung betrug 12,5 Watt bei Burstenergien von 235 mJ 12 mJ (Abb. 6.3.1) und 22 Pulsen im Burst. Die Pulsdauer betrug 50 ns 5 ns mit Pulsenergien von ca. 11 mJ. Bei höheren Pumpleistungen ist eine Astigmatismuskompensation für die Stabilität des Startresonators unumgänglich. Diese könnte durch Benutzung eines asphärischen Startresonatorspiegels erfolgen. Abb. 6.3.2 zeigt das Modenprofil des Lasers bei einer mittleren Ausgangsleistung von 12,5 Watt. Es ist gut zu erkennen, daß der Mode einen Astigmatismus aufweist.
Abb. 6.3.3 zeigt einen typischen Intensitätsverlauf
und seine Fouriertransformierte.
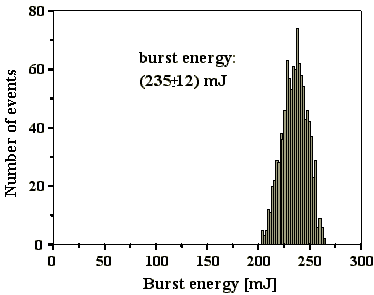
Abb. 6.3.1: Histogramm der Burstenergien bei 2,08 kW
Pumpleistung

Abb. 6.3.2: Modenprofil bei einer mittleren Ausgangsleistung
von 12,5 W
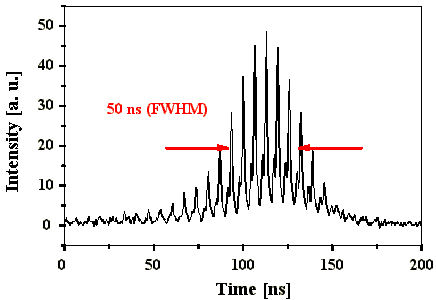
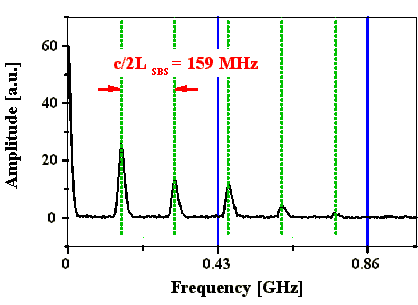
Abb. 6.3.3: Zeitstruktur und Fouriertransformierte eines Pulses des kompakten
SBS-Resonators
(blaue Linien entsprechen Frequenzabständen nB
)
Im Rahmen dieser Diplomarbeit wurde die Abhängigkeit der
Pulsenergien und der Pulsstabilität sowie der longitudinalen
Frequenzstruktur von verschiedenen Parametern untersucht. Die
Tabelle gibt eine Übersicht über die variierten und
konstant gehaltenen Parameter und die verwendeten SBS-Medien.
Die Resonatoren wurden nach den Kriterien der Stabilität
des Startresonators, gleicher Modenvolumina und vergleichbarer
Arbeitspunkte desselben Stabilitätsbereichs berechnet und
realisiert, um die Vergleichbarkeit der Pulsenergien und Standardabweichungen
sowie der longitudinalen Frequenzstruktur zu gewährleisten.
Die Untersuchungen haben gezeigt, daß die Längenanpassung
des Startresonators an die Brillouin-Länge der verwendeten
SBS-Medien zur Schwellabsenkung der SBS beiträgt. Die Brillouin-Länge
ist die Länge eines Fabry-Perot-Resonators mit longitudinalem
Modenabstand des Brillouin-Shifts. Die Pulsenergie und Pulsstabilität
des SBS-Oszillators sind unabhängig von der Länge des
SBS-Resonators. Das Aussetzen der SBS bei einem Verhältnis
von Startresonator zu SBS-Resonator von 2:1 konnte bestätigt
werden.
Es konnte nachgewiesen werden, daß die Modulation der Q-switch
Pulse aus der Schwebung der SBS-Resonatorfrequenzen resultiert.
Ihre spektralen Abstände ergeben sich wie die Frequenzabstände
eines Fabry-Perot-Resonators aus c/2LSBS. Diese spektralen
Abstände korrelieren nur mit der SBS-Resonatorlänge,
sie sind unabhängig von der Startresonatorlänge und
von der Fokussierung im Teleskop.
Durch die Variation des effektiven Reflexionsgrades des Startresonatorspiegels
wurde gezeigt, daß die Modulationstiefe mit steigenden Verlusten
im Startresonator zunimmt. Die Schwebungsfrequenzen der SBS-Resonatorfrequenzen
weisen höhere Amplituden auf. Die Repetitionsrate der Q-switch
Pulse im Burst nimmt mit geringer werdendem effektiven Reflexionsgrad
des Startresonatorspiegels ab, die Pulsenergien werden größer.
Gleichzeitig nimmt die Pulsdauer ab. Der Güteschaltungsprozeß
der SBS startet aus dem ersten Spike des Startresonators heraus.
Die SBS-Schwelle der SBS-Medien hat deshalb keinen entscheidenden
Einfluß auf die Pulsenergie.
Weiterhin konnte nachgewiesen werden, daß die Frequenzverschiebung
durch die SBS abhängig von der Startresonatorlänge ist.
Bei einer leicht verstimmten Startresonatorlänge relaxiert
die Frequenzverschiebung vom Vielfachen des Startresonatormodenabstands
auf die Mittenfrequenz der Brillouin-Linie zu.
Ein wichtiges Kriterium für die Effizienz des SBS-Oszillators
ist der Energiereflexionsgrad des SBS-Spiegels. Die Untersuchung
der Abhängigkeit von den Aberrationen im SBS-Resonator und
dem effektiven Reflexionsgrad des Startresonatorspiegels ergab,
daß der Energiereflexionsgrad mit größeren Aberrationen
sinkt. Das Maximum lag bei einem effektiven Reflexionsgrad des
Startresonatorspiegels M2 von 0,1 bis 0,3. Der Faktor für
Schwellherabsetzung der SBS im Resonator war größer
4.
Im letzten Teil dieser Arbeit wird ein optimierter SBS-Oszillator
beschrieben. Dieser enthält keine Linsen; die starke thermische
Linse des Nd:YALO wird zur Fokussierung in die SBS-Zelle genutzt.
Die Nutzung von CO2 als SBS-Medium ermöglichte
eine kurze optische Resonatorlänge von 1,04 m. Die mittlere
Ausgangsleistung betrug 12,5 Watt bei einer mittleren Pumpleistung
von 2,09 kW. Der Gesamtwirkungsgrad betrug 0.6%.
[1] D. A. Rockwell, IEEE J. Quant. Electron. 24, 1124 (1988)
[2] M. J. Damzen, S. Camacho-Lopez, R. P. M. Green, Phys. Rev. Lett. 76, 2894
(1988)
[3] A. Brignon, J.-P. Huignard, Opt. Commun. 119, 171 (1995)
[4] M. J. Damzen, R. P. M. Green, G. J. Crofts, Opt. Commun. 110, 152 (1994)
[5] M. J. Damzen, M. H. R. Hutchinson, W. A. Schroeder, Opt. Lett. 12, 45 (1987)
[6] G. C. Valley, IEEE J. Quant. Electron. 22, 704 (1986)
[7] B. Y. Zel'dovich, V.I. Popovichev, V.V. Radulisky, F.S. Faisullov, Sov. Phys.
JETP 15, 109 (1972)
[8] D. S. Sumida, D. C. Jones, D. A. Rockwell, IEEE J. Quant. Electron. 30, 2617
(1994)
[9] J. Endriz, J. Haden, D. Mundinger, Diode Array-Pumped Kilowatt Laser, post
deadline paper, CLEO'95 Baltimore,
[10] H. J. Eichler, A. Haase, R. Menzel, IEEE J. Quant. Electron. 31, 1265 (1995)
[11] H. L. Offerhaus, H. P. Godfried, W. J. Witteman, Opt. Commun. 128, 61 (1996)
[12] C. B. Dane, L. E. Zapata, W. A. Neuman, M. A. Norton, L. A. Hackel, IEEE J.
Quant. Electron. 31, 148 (1996)
[13] M. Ostermeyer, A. Heuer, R. Menzel, 27 Watt average output power with 1.2*DL
beam quality from a single rod Nd:YAG-Laser with phase conjugating SBS-mirror,
to be published
[14] A. Kummrow, R. Menzel, D. Schumann und H. J. Eichler, International Journal
of Nonlinear Optical Physics 2, 261 (1993)
[15] D. Schumann, Studienarbeit am Optischen Institut der TU Berlin (1990)
[16] A. Kummrow, R. Menzel, D. Schumann, Resonant emission of solid state lasers
with stimulated Brillouin scattering, to be published
[17] N. Hodgson, H. Weber, Optical Resonators, Springer Verlag (1997)
[18] W. Kaiser, M. Maier, in "Laser Handbook", cds: F.T. Arrechi, E.O. Schulz-Dubois,
North Holland, Amsterdam
[19] A. Yariv, R. A. Fisher, "Optical Phaseconjugation", ed.: Fisher, Academic Press
(1983), New York
[20] A. Kummrow, H. Meng, Optics Communications 83, 342 (1991)
[21] G. G. Kochemasov, V. D. Nikolaev, Sov. J. Quant. Electron. 7, 60 (1977)
[22] H. J. Eichler, R. Menzel, D. Schumann, Appl. Opt. 31, 5038 (1992)
[23] H. J. Eichler, R. König, H.-J. Pätzold, J. Schwartz, Appl. Phys. 61, 73 (1995)
[24] N. F. Andreev, E. Khazanov, G. A. Pasmanik, IEEE J.Quant. Electron. 28, 330
(1992)
[25] A. Agnesi, G. C. Reali, Opt. Commun. 89, 41 (1992)
[26] P. J. Soan, M. J. Damzen, V. Aboites, M. H. R. Hutchinson, Opt. Lett. 19, 783
(1994)
[27] R. P. M. Green, G. J. Crofts, W. Hubbard, D. Udaiyan, D. H. Kim, M. J. Damzen,
IEEE J. Quant. Electron. 32, 371 (1996)
[28] Y. Jigguo, J. Hongwei, Opt. and Quant. Electron. 26, 929 (1994)
[29] N. N. II'ichev, A. A. Malyutin, P. P. Pashinin, Sov. J. Quat. Electron. 12, 1161
(1982)
[30] H. Meng, H. J. Eichler, Opt. Lett. 16, 569 (1991)
[31] D. C. Hanna, C. G. Sawyers, M. A. Yuratick, Opt. and Quant. Electron. 13, 493
(1981)
[32] D. Pohl, Phys. Lett. 24, 239 (1967)
[33] W. Koechner, Solid state laser engeneering, Springer Verlag (1996)
[34] Weber, "Laserphysik", Skript zur Vorlesung "Quanten- und Korpuskularoptik",
FLI Berlin GmbH
[35] F. K. Kneubühl, M.W. Sigrist, Laser, Teubner-Verlag (1991)
[36] D. M. Pepper, Opt. Engineering. 21, 156 (1982)
[37] G. Giuliani, M. M. Denariez-Robergè, P.-A. Bèlanger, Appl. Opt. 21, 3719 (1982)
[38] M. D. Skeldon, R. W. Boyd, IEEE J. Quant. Electron. 25, 588 (1989)
[39] P. A. Bèlanger, A. Hardy, A. E. Siegman, Appl. Opt. 19, 602 (1980)
[40] J. Auyeung, D. Fekete, D. M. Pepper, A. Yariv, IEEE J. Quant. Electron. 15, 1180
(1979)
[41] M. J. Damzen, IEEE J. Quant. Electron. 23, 457 (1987)
[42] D. Schulze, Eigenschaften phasenkonjugierender SBS-Zellen für Festkörperlaser,
Diplomarbeit an der TU Berlin, 1992
[43] Messungen von A. Heuer und J. Schultheiß, AG Photonik, Uni Potsdam
[44] M. Kramer, Erzeugung kurzer Laserimpulse durch stimulierte Brillouin-Streuung in
einem instabilen Laserresonator, Dissertation, Fr.-Schiller-Universität Jena, 1995
[45] Demtröder, Laserspektroskopie, 3. Auflage, Springer Verlag Berlin (1993)
[46] E. Geinitz, Diplomarbeit am optischen Institut der TU Berlin (1994)
[47] K. Mittler, M.Ostermeyer, Longitudinal mode structure of Nd-lasers
with phase conjugating mirrors based on stimulated Brillouin scattering in
different materials, CLEO '97 Baltimore, poster session
[48] J. Schultheiß, Phasenkonjugierende Spiegel auf der Basis der stimulierten
Brillouin-Streuung für kleine Pumpleistungen, Diplomarbeit an der Uni Potsdam
(1997)
[49] M. Dahl, Optimierung der Resonatorlängen eines Nd:YAG-Lasers mit
phasenkonjugierender SBS-Zelle, Diplomarbeit an der TU Berlin, 1995
[50] R. Scherrer, Nd:Cr:GSGG-Laser mit phasenkonjugierendem SBS-Spiegel,
Diplomarbeit an der TU Berlin, 1994
[51] R. A. Lamb, M. J. Damzen, J. Opt. Soc. Am. 13, 1468 (1996)
[52] P. Narum, M. D. Skeldon, R. W. Boyd, IEEE J. Quant. Electron. 22, 2161 (1986)
[53] M. J Damzen, R. A. Lamb, G. K. N. Wong, Opt. Commun. 82,
337 (1991)
Ich danke...
...Herrn Prof. Dr. Ralf Menzel für die Unterstützung
bei der Anfertigung dieser Arbeit.
...Herrn Dipl.-Phys. Martin Ostermeyer für seine Betreuung, für die überaus lehrreichen
Gespräche und Diskussionen und für seine Geduld.
...Herrn Dr. Norman Hodgson für die Korrektur meiner Diplomarbeit, die anregenden
Diskussionen und spaßigen Einlagen.
...Herrn Dipl.-Phys. Axel Heuer und Dipl.-Phys. Dieter Lorenz für die anregenden
Diskussionen und Show-Einlagen. Sie haben das Arbeitsklima entscheidend
geprägt.
...der Familie Scharfenorth für ihre Unterstützung in Sachen Resonatorkomponenten,
insbesondere bei der Vorbereitung auf die Lasermesse '97.
...meiner Mutter und meiner Schwester für die moralische
und finanzielle Unterstützung.

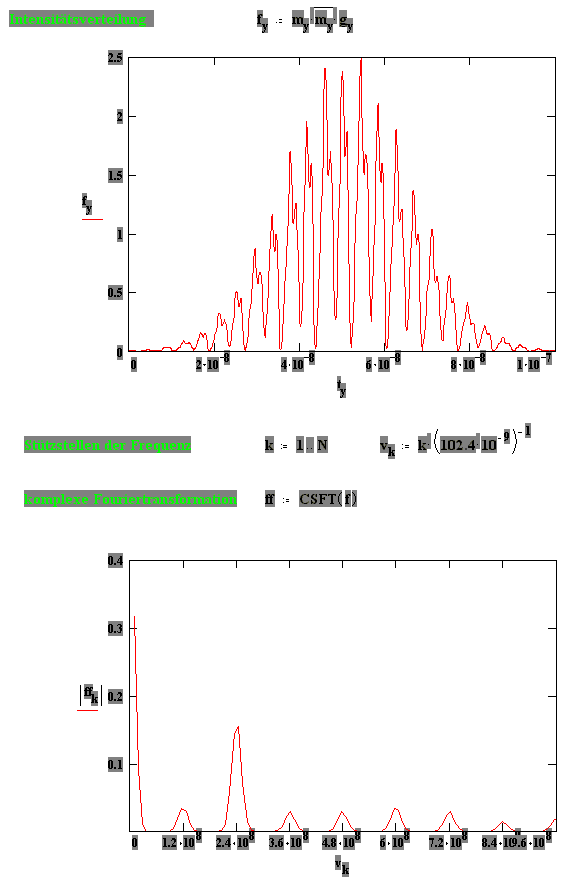
Selbständigkeitserklärung
Hiermit erkläre ich, daß ich diese Arbeit selbständig und nur unter Verwendung
der angegebenen Quellen angefertigt habe.
Berlin, den 09.08.97 ___Kay Mittler__